【2023国赛C题】基于正态预测与多约束规划的蔬菜补货与定价模型
记录一下今年乱写的文章，用来给我空荡荡的博客撑撑场面：）
摘要
生鲜商超都会对蔬菜类商品有补货计划，但由于蔬菜类商品的保鲜期一般较短，且部分品种若当日未售出则隔日无法再售。对于商超而言，若售价过高或进货量过多导致商品剩余则会导致浪费，若进货量太少则不能满足市场需求，售价过低则不能实现满足商超的利润最大化。因此，探究商超的补货计划与定价方案具有重要意义。
首先对附件中的数据进行预处理，剔除对整体数据影响不大的干扰类数据，接着对商品的流水数据进行整理，用于后续数据分析处理。
第一问，首先将历史数据分别按照日与年投影，得到每个品类销售量在一天和一年内的分布频率。其次，我们对销售量进行时间序列分解，得到影响销量的趋势因素、季节因素及残差因素。之后，为探究不同品类的相关性，对品类数据两两拟合，依据拟合优度的好坏对各品类进行多元线性拟合，从而得到品类之间的关系。对于各单品，我们以日均销售量、平均单次销量、销量的方差、平均销售时间作为特征变量进行$k - means$聚类，通过聚类结果散点图确定单品分布规律，最后进行回归确定相互关系。
第二问，首先对该商超的定价方式进行分析，找到影响定价的两个因素：批发成本价和目标利润率，并调整受到损耗率影响的定价模型。之后，根据往年6月，7月的成本数据作为数据样本，使用蒙特卡罗模拟预测出目标日期的成本变动情况，再根据往期目标利润率和样本时间内对菜品的需求量进行回归拟合，得到市场在给定的利润率下对菜品的需求关系。将如上的关系式代入至最终的有关利润的目标函数中，对目标函数进行求解，得到目标时间内菜品的定价计划和补货计划。
第三问，考虑到更多的决策变量与更复杂的约束条件，我们采用更合适的多约束目标规划的方法进行求解。为了有效地刻画销售量，我们将市场需求量视为受价格影响均值的正态分布，从而建立进货量与销售量的关系；接着，我们使用指数平滑法对未来成本进行估计；进一步，我们从补货量、品类、市场需求等多方面建立约束条件，完成对目标规划的构建，最终求解其最优值。
第四问，为了找到更多影响商超补货量与定价的因素，我们从商超运营的外部因素和内部因素进行分析，找到供货商，运货商和超市内部运营人员这三个因素。再根据商超利润的目标函数，定性给出以上影响因素与商超收益的关系。
关键词：补货与定价计划；多元回归拟合；聚类分析；多约束规划；蒙特卡罗模拟
一、问题的提出
1.1 问题背景
现如今市场中的蔬菜类商品由于保质期限短、耐存储性差，进货渠道多、规模大，需要商超每日进行补货与定价工作。补货数量需要在蔬菜品种与进价不确定的情况下，根据历史数据与需求状况做出决策。定价则采取成本加成法，依据商品的成本与利润进行定价。补货与定价的决策与有效的市场分析密切相关，通常要考虑商品销量与时间的关系及空间限制下销售组合的合理性问题。
1.2 问题重述
现有一商超经销蔬菜，已经确认六大蔬菜品类中各商品的具体信息。根据给出数据，得到六种蔬菜品类于2020年7月1日至2023年6月30日的销售动态明细与批发价格情况。同时得到了蔬菜近期运损或变质的损耗率数据。
先建立模型解决以下问题：
（1）从需求端来看，分析蔬菜间大类品种不同或单品种类不同之间存在的相关联性，在此基础之上研究各蔬菜品种与单品销售数量的分布规律及相互关系。
（2）基于以品类为单位的补货计划，分析蔬菜品类间销售总量、成本加成定价之间的关系；同时分析出在未来一周即2023年7月1-7日，可使商超收益最大化的每日补货总量与定价决策。
（3）由于商超的销售空间有限，分析制定使售卖单品总量控制在27到33个、各单品进货数量为最小陈列量2.5千克的补货计划。基于2023年6月24到30日的可出售品种，分析如何制定7月1日单品补货数量及定价决策，可达成在满足市场需求的情况下实现收益最大化。
（4）分析影响补货数量与定价决策的其他因素，分析该因素的数据可为决策提供哪些帮助，充分说明建议与理由。
二、问题分析
2.1问题一的分析
对于问题一，题目要求分别以品类和单品为对象，给出品类和单品日销售量的分布规律与相互关系。
以品类为对象时，我们首先对附表2进行处理，对六种品类的销售量汇总，将品类与单品的时间序列分布的销售明细按一天内时间和一年内周期进行刻画和描述，得到品类的销售分布。之后，在分析不同品类之间的相互关系时，直接拟合来分析品类之间关系可能会导致拟合优度过差。于是采用一元拟合与多元拟合相结合的方式，首先使用一元拟合判断各个品类之间相关度，对数据进行剔除筛选后，对六个品类使用多元拟合分析得到品类之间的相关关系。当对象为单品时，首先根据每个单品销售量的特征进行聚类分析，得到分布特征相似的六类，再采用与品类分析相似的方法对六类单品进行分析。
2.2问题二的分析
对于问题二，题目要求以品类为单位，给出一周内的订货计划。
首先明确该商超的定价方式，给出定价与可变成本，损耗率与目标利润率之间的关系。之后，根据两年来成本变动的数据样本，使用蒙特卡洛模拟预测出接下来一周内的成本。然后，通过回归拟合找到各个品类成本与定价之间的关系，将以上关系到带入到与利润有关的目标函数中去，最终得到以目标利润率为自变量的完整的目标函数。通过对成本的多次预测减少误差，最终得到品类的补货计划与定价计划。
2.3问题三的分析
对于问题三，题目要求我们根据 2023年 6 月 24-30 日的可售品种，给出 7 月 1 日的单品补货量和定价策略，在尽量满足市场对各品类蔬菜商品需求的前提下，使得商超收益最大。本问有明确的目标（商超收益最大）与较多的约束条件（单品总数、最小订购量等），故可看做多约束的目标规划问题。我们使用销售量的均值与方差对蔬菜市场需求进行刻画，接着使用概率密度的积分确定销售量与补货量的关系，得到简化后的目标函数。最后代入程序求解，即可得出最优的单品补货量和定价策略。
2.4问题四的分析
对于问题四，题目要求给出影响定价与进货的其它因素，并说明有哪些优点与帮助。
我们给出了三个有关的数据：供货商，运货商和商超人员配置。综合考虑了供货商，运货商对固定成本和损耗率的影响，以及人员配置的效率对售货的影响。并给出了以上因素对目标函数和约束条件的影响。
三、模型假设
3.1假设一
假设品类或单品销售量之间存在一定的关系，且这样的关系是线性的。
3.2假设二
历史数据和未来数据存在相关性，以历史数据模拟未来数据的做法是可靠的。
3.3假设三
假设大量数据中存在的数据特点以及整体趋势不会因为某些特定数据的改变而发生显著性改变。
3.4假设四
假设偶然因素对商品销售量的影响情况是正态分布的，蒙特卡罗模拟对销售量的正态模拟是可信的。
四、符号说明
| 符号定义 | 符号说明 |
|---|---|
| $$X_{i}$$ | 品类的日销售量 |
| $$X_{i}$$ | 单品的日销售量 |
| $${\widehat{\beta}}_{0i}$$ | 观测品类的截距期望值 |
| $${\widehat{\beta}}_{ni}$$ | 第n个剩余品类销售量对于第i个选定品类销售量的期望系数数据变换矩阵 |
| $$U_{ij}$$ | 回归拟合后的残差值 |
| $$R_(i j)²$$ | 拟合优度 |
| $$C_{i}$$ | 商品成本 |
| $$C_{varible}$$ | 可变成本 |
| $$C_{fixed}$$ | 固定成本 |
| $$ V $$ | 销售总量 |
| $$R_{damage}$$ | 损耗率 |
| $$R_{t}$$ | 目标利润率 |
| $$\rho_{i}$$ | 商品损耗率 |
| $$T_{i}$$ | 补货量 |
| $$P_{i}$$ | 商品价格 |
五、问题一模型的建立与求解
5.1数据预处理
5.1.1 样本剔除
根据题目信息可知，蔬菜商品由于保鲜期短及长途运输会出现品相变差或是运损问题，对于该部分商品商超采取打折销售的方式处理。为了更直观地探究蔬菜间大类品种不同或单品种类不同之间的关联关系，考虑到打折销售的商品在商品总数中占比不大且属于特殊情况，不会对整体的分析结果产生显著影响，因此将附件2中关于此类商品的信息剔除表格。同理，这里也对退货商品的数据进行同
5.1.2销售量汇总
附件2提供了所有单个商品的销售瞬时信息与批发价格情况，为了刻画不同单品之间的相关性、便于对任意单品变量进行分析，这里将每个单品每日的销售量进行汇总，得到251个单品的日销量表；同时，为了揭示不同品类之间的相互关系、便于对同一品类的商品进行分析，这里将每个品类的日销售量汇总，得到了6个品类的日销售量汇总。下面进行进一步的模型建立与数据处理。
5.2分布规律分析
5.2.1整体分析
为了能进一步探究各品类之间的相互关系，首先要分析各蔬菜品类销售量的分布规律。根据剔除异常样本及同品类销售量加和后的处理数据，我们首先绘制了2020年7月1日至2023年6月30日各蔬菜品类单日销售额随日期变化的走势图。
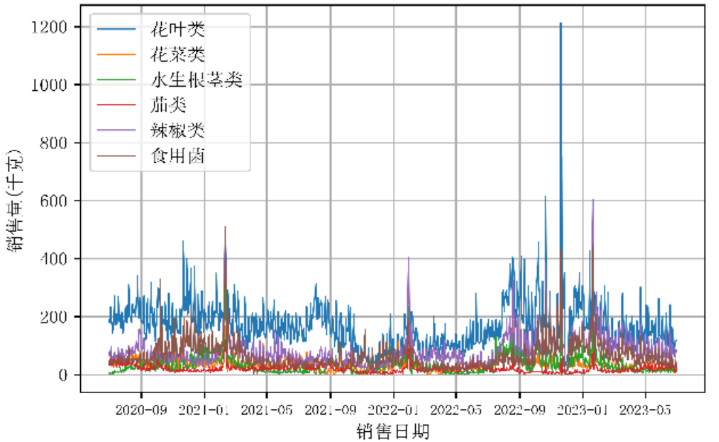
图1:六种品类销售量随日期变化曲线图
根据图1我们可以发现该商超各类蔬菜品类的日销售额大多集中在0-200千克。每年的12月至次年二月，蔬菜销售额会有明显的集中趋势，说明冬季的蔬菜销量较每年的其他时节会有明显增加。此外，花叶类蔬菜常年保持较高的销售额，可能与该商超花叶类蔬菜品质好或地方口味偏好有关。
上述图1虽定量地表示了六种品类近年来的销售量走势情况，但不易于直观反映蔬菜销售量的年度趋势及一天当中的变化情况，也就难以进一步揭示他们间的相互关系，因此，我们从年度和单日两个维度进一步探究蔬菜品类的分布规律，更加直观地反映蔬菜销售量的数据变化情况。
5.2.2单日分析
我们通过对同时段不同品种的蔬菜销售量进行数据处理，得到了各时段的每日销售数量总和，绘制了单日各时间段销售额占比的频率分布图，其中蔬菜总体的分布图如下：
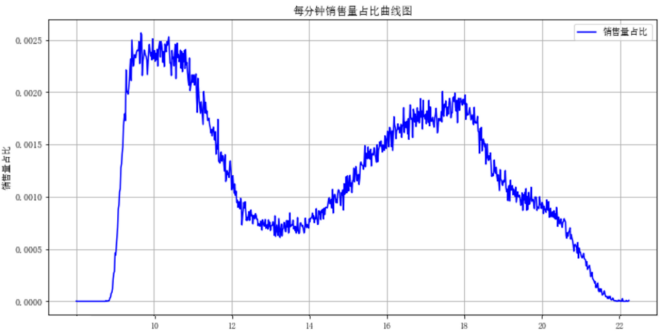
图2:单日不同时间段销售量占比曲线图
从图2我们可以得到，单日销售量分布集中趋势主要在上午9点至11点，次高峰为下午17点至18点，这些时间段处于午饭及晚饭前，菜品需求较大，销售量占一天中的比例更高。
为了对分析各品类之间的相互关系提供支撑数据，我们对单日不同时段销售量占比的分析由总体加和细分到六个品类，六类蔬菜单日各时间段销售额占比的频率分布图分别如下：
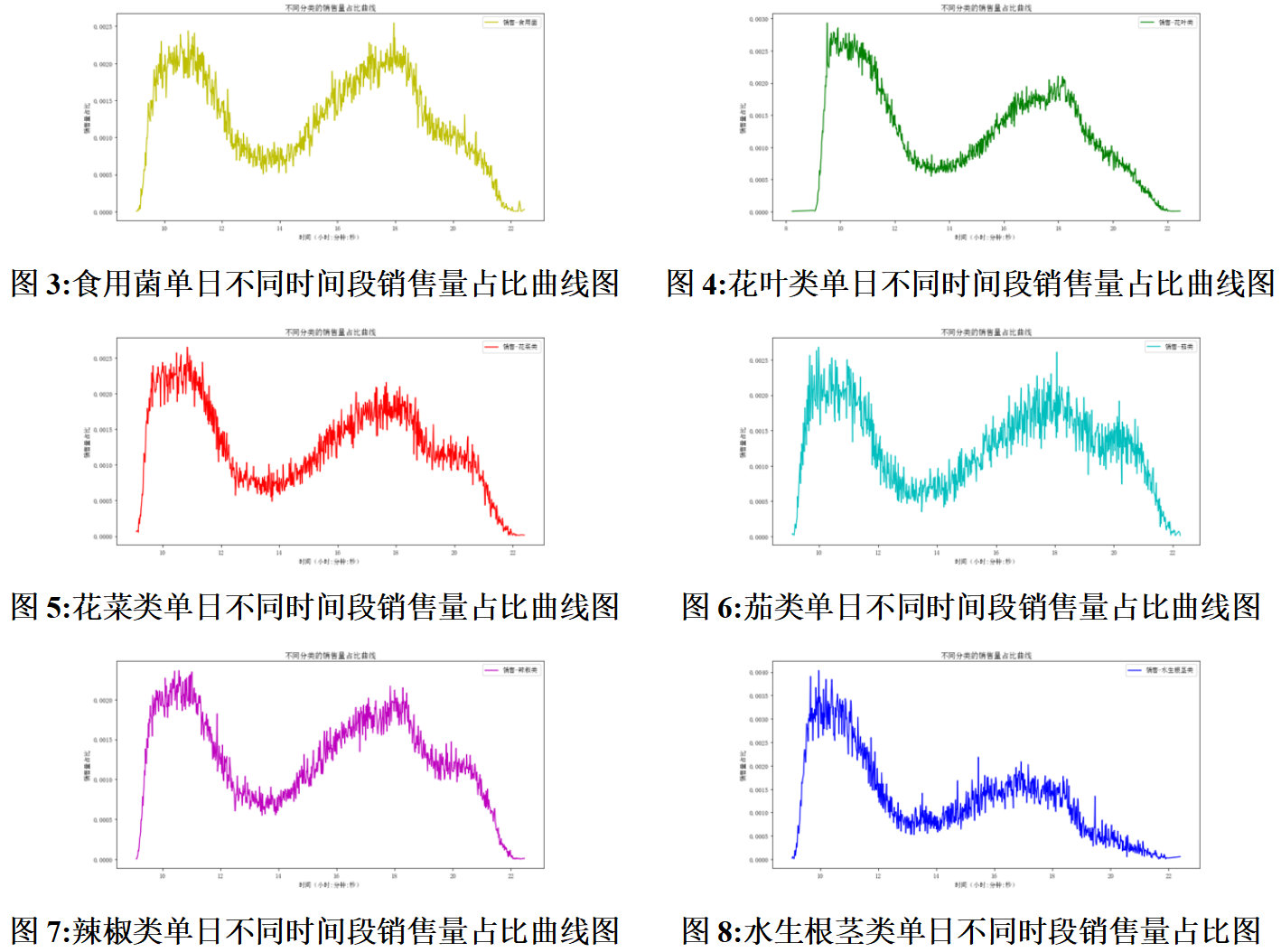
观察六张分布图我们可以发现，各品类之间分布情况与曲线走势大致相近，同时均与图2六类总体在单日不同时段销售额占比曲线相近，但也存在一定的差别，例如：水生根茎类于下午17点至18点的销售量较总体品类于该时段销售量明显呈离散状态，可能是水生根茎类商品保鲜能力差，午后品相较差所致。
5.2.3年度分析
对六类蔬菜的销售额走势进行了时间序列分解，将销售额的变动看作由趋势因素、季节性因素以及残差因素这三个因素共同影响造成的。以图线的形式展示的六类蔬菜各个因素的影响情况如下：
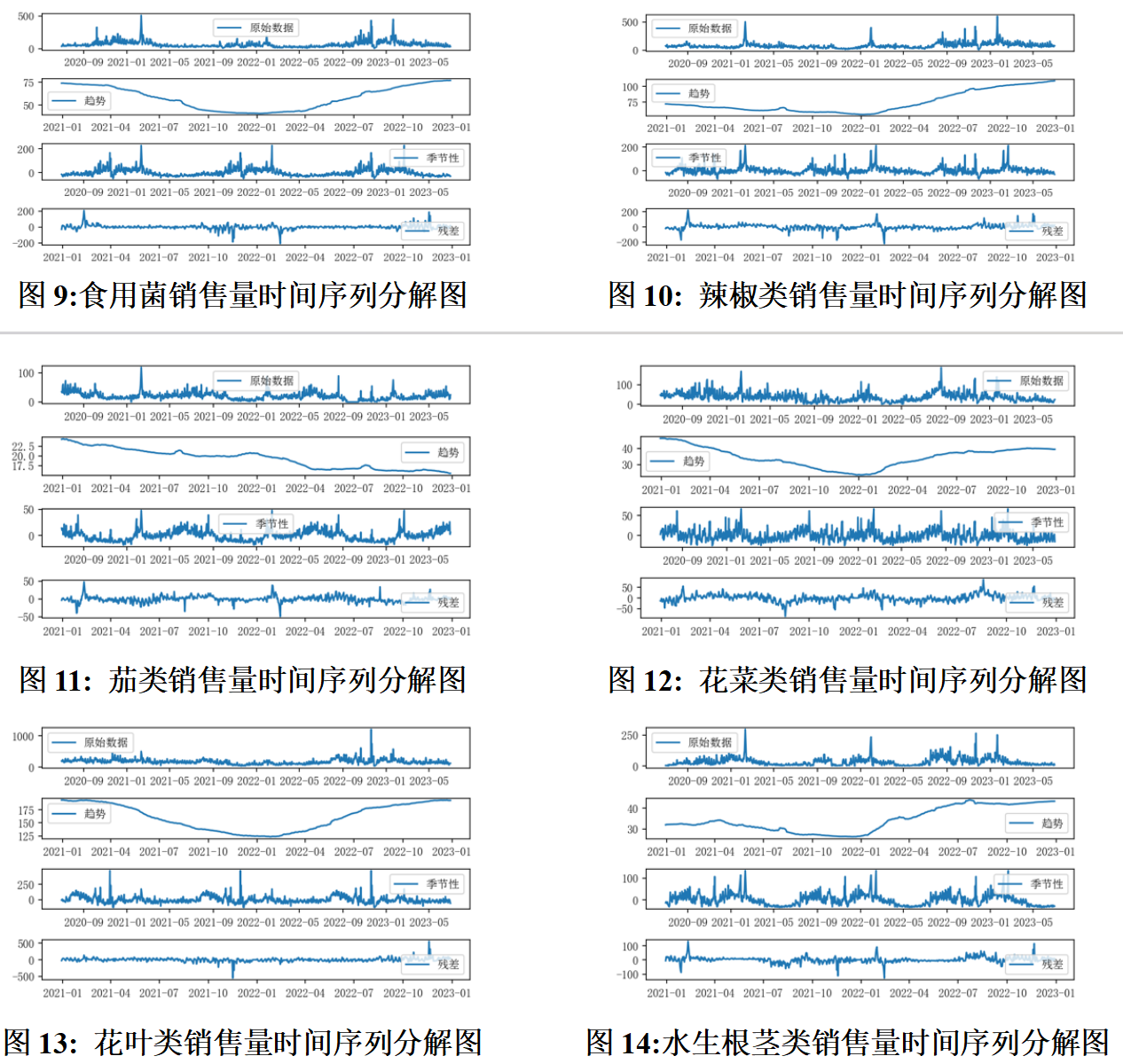
上述图表反映了六种蔬菜品类因不同影响因素造成的销售量走势情况，具体分析如下：
在长期趋势方面，除茄类外的五类蔬菜均有类似的长期趋势，即均从高位销量逐步下降，并均于2022年1月降至趋势最低点，随后又一路攀升至高位。茄类的趋势整体呈长期下降状态，由2021年1月的最高点降至2023年1月的最低点。
在季节性因素方面，与整体分布规律类似，各类蔬菜均体现出明显且相近的季节性变化，可见蔬菜产品的时令性较强。具体体现在各蔬菜品类销售额的季节因素通常在冬季达到峰值，而在夏季处于底位水平。
在残差因素方面，各类蔬菜的残差因素均长期接近于零并在一定范围内波动，偶尔会出现一定程度的震荡而产生极个别峰值与谷值。可见，时间序列的分解效果较好，未出现明显的残差项。
5.3一元回归拟合模型的建立
针对要研究不同品类或不同单品间存在的相关性，我们首先将问题简单化，先研究每两个品类或单品之间其日销售量的是否存在较强的相关联性。任取某两个品类i和j，对其进行二元回归拟合分析：
$$
\widehat{X_i} = \widehat{\beta_{0ij}} + \widehat {\beta_{1ij}} X_j + U_{ij}
$$
其中，$X_{i}$与$X_{j}$是两种品类或单品的日销量数据，$\widehat{\beta_{0ij}}$表示的是$X_{i}$的截距期望值，$\widehat {\beta_{1ij}}$表示的是第j个自变量销售量对于第i个品类销售量的的期望系数，$U_{ij}$是回归拟合后的残差值。同时，我们可得到两种品类或两种单品间配对的$R_(i j)²$。
分别对六种品类进行两类一组的模拟回归后，则可以得到六个品类两两对应的$R_(i j)²$值：
$$
R^2 = 1 - \frac{SSR}{SST}
$$
其中，$SSR$是拟合数据的回归平方和，表示回归模型的拟合误差；$SST$是拟合数据的总平方和，表示总体数据的离散程度。
最终可以得到六种品类两两之间的数据拟合结果，如下：
表1:六个品类销售量二元回归拟合结果
| 水生根茎类 | 花叶类 | 花菜类 | 茄类 | 辣椒类 | 食用菌 | |
|---|---|---|---|---|---|---|
| 水生根茎类 | 1 | 0.3505 | 0.3440 | 0.0188 | 0.4410 | 0.4440 |
| 花叶类 | 0.3506 | 1 | 0.4090 | 0.1078 | 0.4099 | 0.4148 |
| 花菜类 | 0.3411 | 0.4090 | 1 | 0.1068 | 0.3289 | 0.3046 |
| 茄类 | 0.0188 | 0.1078 | 0.1068 | 1 | 0.1150 | 0.0310 |
| 辣椒类 | 0.4410 | 0.4098 | 0.3289 | 0.1150 | 1 | 0.4638 |
| 食用菌 | 0.4440 | 0.4148 | 0.3046 | 0.0310 | 0.4638 | 1 |
其中，相同数据之间的相关性为1。由于部分数据拟合的结果不佳（R²值过低），在后续的多元回归拟合中会对选用拟合的自变量进行选择调整。
5.4多元回归拟合模型的建立
对于给定的六个蔬菜品类，要探究分析彼此之间销售量可能存在的关系。其中，针对任一种品类而言，剩余五种品类均可能对其产生关联性的影响，因此我们可将六个品类依次设为因变量，剩余五种品类则相应定为自变量，我们假定每一个因变量对自变量的影响都是线性的，即在其他自变量不改变的情况下，因变量的均值随自变量的变化而均匀变化。这种包含多个因变量且其共同影响着一个自变量的问题，我们可以通过多元回归拟合的方法来解决。因此，我们建立数学模型如下：
$$
\widehat{Y_i} = \widehat{\beta_{0i}} + \widehat{\beta_{1i}} X_{i1} + \widehat{\beta_{2i} }X_{i2} + \widehat{\beta_{3i} }X_{i3} + \widehat{\beta_{4i} }X_{42} + \widehat{\beta_{5i} }X_{i5} + U_{i}
$$
这便是针对问题一应用的总体回归模型。其中，$\hat{Y_i}$表示第i个蔬菜品类销售量的观测值为因变量；$\widehat{\beta_{0i}}$与$\widehat{\beta_{1i}}$作为回归系数，分别表示的是$\hat{Y_i}$的截距期望值及第n个剩余品类销售量作自变量对于第i个选定品类销售量的期望系数；$X_{it}$表示的是与$\hat{Y_i}$相关的第t个商品的销售量。
为了探究出六大品类销售量之间存在的关系，我们要依次将每一品类的销售量与剩余五个品类销售量依次进行拟合，应用上述的回归模型对因变量作出推测，最终得到各品类之间的线性关系。
要注意，两两品类之间并不一定存在强线性相关，换言之，每一个$\widehat{\beta_{i}}$所对应的拟合优度不一定都是满足要求的，因此参考5.3由一元回归拟合模型得出的两两变量之间的相关度R²，将每组拟合结果中R²最低的值剔除。
在使用$MATLAB$进行六个品类的回归拟合之后，得到的品类销售量之间关系如下：
表2:六个品类多元回归拟合结果
| 种类 | 多元回归方程 | 拟合优度 |
|---|---|---|
| 水生根茎类 | $\widehat{Y_1}$= -7.9593 + 0.031584$X_{1} $+ 0.27019$X_{2} $+ 0.17478$X_{5}$+ 0.17478$X_{6}$ | R²=0.5615 |
| 花叶类 | $\widehat{Y_2}$= 65.0666 + 0.21516$X_{1}$+ 1.1308$X_{1} $+ 0.36025$X_{5} $+ 0.36025$X_{6}$ | R²=0.5643 |
| 花菜类 | $\widehat{Y_3}$= 5.8357 + 0.17117$X_{1} $+ 0.10516$X_{2}$+ 0.061405$X_{4} $+ 0.061405$X_{5}$ | R²=0.4887 |
| 茄类 | $\widehat{Y_4}$= 9.74 + 0.030363$X_{1} $+ 0.10096$X_{2}$+ 0.070306$X_{5}$+ 0.070306$X_{6}$ | R²=0.1717 |
| 辣椒类 | $\widehat{Y_5}$= 11.3049 + 0.44668$X_{1} $+ 0.13515$X_{2} $+ 0.24772$X_{3} $+ 0.24772$X_{6}$ | R²=0.5862 |
| 食用菌 | $\widehat{Y_6}$= -1.5826 + 0.44473$X_{1} $+ 0.1443$X_{2} $+ 0.10649$X_{3}$+ 0.10649$X_{4}$ | R²=0.5856 |
由拟合优度可以看出，某一种品类和其它几种品类存在一定的关联性，但都不显著。此外，在回归方程最优的情况下，茄类与其它菜品品类的拟合优度值最低，拟合值仅有0.1717，也就是说，茄类的销售量和其它几类菜品的销售量几乎无关。
5.5单品的聚类分析
5.5.1 $k - means$聚类算法模型
由于直接对200余种单品进行一元或多元线性回归分析的计算量过大，其中又有许多种类往往具有相近的分布规律，于是我们决定采用聚类分析对每个单品之间的关系进行求解。首先，根据附件2中每个单品的销售信息，提取单品销售量的数据特征，在对单品进行聚类分析后，再研究不同蔬菜单品销售量的分布规律。
我们使用$k - means$聚类算法进行分析。$k - means$聚类算法是一种常用的无监督学习算法，用于将数据集中的数据点划分成$K$个不同的簇，以使每个数据点都属于最近的簇中心点所代表的簇。其具体的计算求解步骤如下：
| K-means 算法求解规程 |
|---|
| Step1：从 n个数据对象任意选择 k个对象作为初始聚类中心 |
| Step2: 循环 Step3 到 Step4 直到每个聚类不再发生变化为止 |
| Step3: 根据每个聚类对象的均值（中心对象）,计算每个对象与这些中心对象的距离,并根据最小距离重新对相应对象进行划分 |
| Step4: 重新计算每个（有变化）聚类的均值（中心对象） |
| Step5: 求得满足方差最小标准的 k 个聚类 |
5.5.2算法求解——肘部法
$k - means$算法需要提前确定聚类的簇数$k$，而$k$值的确定则需要用到肘部法来求解，即通过改变聚类数量计算并绘制出损失函数，找到函数拐点位置。在使用肘部法确定聚类$k$值时需首先确定核心指标$SSE$（误差平方和）：
$$
SSE = \sum_{i = 1}^{k}{\ \sum_{p\epsilon C_{i}}^{}\left| p - m_{i} \right|^{2}}
$$
其中，$C_{i}$是第i个簇，$p$是$C_{i\ }$中的样本点，$m_{i\ }$是$C_{i\ }$的质心（即$C_{i\ }$中所有样本的均值），SSE是所有样本的聚类误差，代表了聚类效果的好坏。手肘法的核心思想是：随着聚类数$k$的增大，样本划分会更加精细，每个簇的聚合程度会逐渐提高，随即误差平方和SSE自然会逐渐变小。同时，当$k$小于真实聚类数时，由于$k$的增大会导致每个簇的聚合程度大幅增加，故SSE的下降幅度会很大；而当$k$到达真实聚类数时，再增加$k$所得到的聚合程度回报会迅速变小，所以 SSE 的下降幅度会骤减，再随着$k$值的继续增大而趋于平缓，也就是说SSE和$k$的关系图是一个手肘的形状，而这个肘部对应的$k$值就是数据的真实聚类数。
我们绘制的肘部法则图形如下：
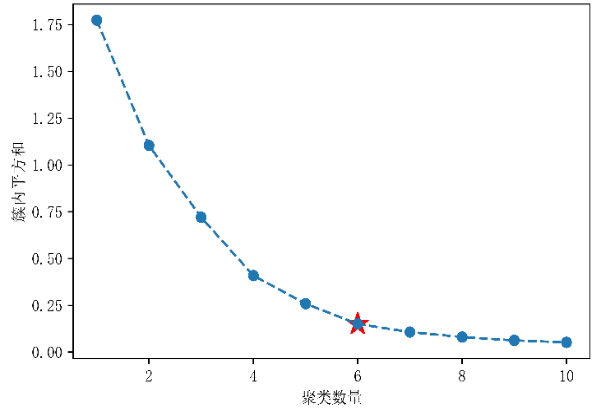
图15:K值求解—肘部法则图像
通过观察我们发现，当$k = 6$时，图像中存在着一个拐点；当$k\epsilon(1,\ 6)$时，曲线急速下降；当$k > 6$时，图像曲线明显趋于平稳。根据肘部法可判断出拐点就是$k$的最佳值，因此本题最佳聚类簇数为6。
5.5.3聚类结果
关于聚类结果的分析，我们使用四个特征变量作为聚类的指标，分别为：日均销售量、平均单次销售量、销售量的方差、平均销售时间。
表3:六个簇类对象均值的相关数据
| 簇序号 | 日均销售量(kg) | 平均单次销量(kg) | 销量的方差(kg²) | 平均销售时间(min) |
|---|---|---|---|---|
| 0 | 1.313 | 0.589 | 0.089 | 818.347 |
| 1 | 0.003 | 0.656 | 1.152 | 1134.378 |
| 2 | 0.863 | 0.717 | 0.058 | 951.609 |
| 3 | 0.182 | 4.878 | 616.609 | 1017.560 |
| 4 | 0.001 | 0.435 | 0.536 | 651.839 |
| 5 | 2.438 | 0.629 | 0.117 | 891.104 |
*“平均销售时间（分钟）”记录销售时刻到当日零点的时间长度
接着，我们选取了三个特征变量，绘制了聚类结果的三维可视化散点图，如下：
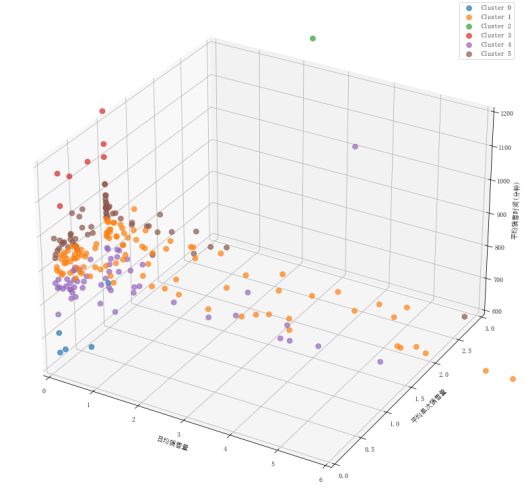
图16:三维可视化聚类结果散点图
观察散点图我们可以发现：类型1、3、4数据点个数较少，数值大小比较极端；类型0、2、5数据点个数较大，数值大小较为常见；类型2区别于类型0和类型5的地方在于其每天销售时间较晚；类型5相较于类型0和类型2的而言平均单次销售量较大；类型0区别于类型2和类型5的地方在于其每天销售时间较早且销售量较低。
5.6聚类后的多元回归拟合
聚类后的单品之间同样存在一定的线性联系。现采用与5.4类似的回归方法，首先计算出两两之间的相关性，通过剔除相关性较低的数据，最终得到回归方程结果，体现了不同单品之间的线性关系。
表4:聚类后的多元回归拟合模拟结果
| 种类 | 回归方程 | 拟合优度 |
|---|---|---|
| 聚类1 | $t_{1}$= 34.5756 + 0.015476 *$Z_3 $+ 0.27019 *$Z_{6}$ | R²=0.4224 |
| 聚类3 | $t_{2}$= -8.6812 + 0.012709 *$Z_1 $+ 0.16653 *$Z_{6}$ | R²=0.5643 |
| 聚类6 | $t_{3}$= 59.149 + 1.7161 *$Z_1 $+ 1.7161 *$Z_{3}$ | R²=0.4887 |
六、 问题二模型的建立与求解
6.1成本加成定价
针对问题二，为了分析蔬菜销量与成本加成定价的关系，我们先研究成本加成定价法，该方法即先估计单位产品的变动成本，再估计产生的固定费用，并按照预期产量把固定费用分摊至各个单位产品，接着在此基础上算入单位变动成本，即可求出全部成本，最后将全部成本与按目标利润率计算的利润额求和，便得到了销售定价。
当销量增加时，每个已售出的商品所分摊的固定成本将减少，同时在可变成本不变且保证要求的利润率不变的情况下，商品的销售定价会降低。反之，当销量减少时，要求的销售定价就会增加。
成本加成法的基本公式如下：
$$
P = \left. （C_{varible} + \frac{C_{fixed}}{V} \right.） \times \frac{1}{\left( 1 - R_{damage} \right)} \times \left( 1 + R_{t} \right)
$$
其中，$C_{varible}$为可变成本，$C_{fixed}$为固定成本，V是销售总量，$R_{damage}$是损耗率，$R_{t}$是目标利润率。同时，我们将固定成本的分摊视作为利润率的补偿。
对于第i个商品，上式可写做：
$$
P_{i} = h(C_{i}，R_{i})
$$
其中，$P_{i}$是第i个商品的价格，$C_{i}$是第i个商品的可变成本，$R_{i}$是第i个商品的定价。该式表示的是定价为可变成本与目标利润率的函数。
在考虑蔬菜损耗时，我们将损耗率视作是目标利润率的补偿。根据附表4，可以推算出损耗对六品类目标利润率的补偿率如下:
表5:六个品类目标利润率补偿率
| 水生根茎类 | 花叶类销量 | 花菜类销量 | 茄类销量 | 辣椒类销量 | 食用菌销量 |
|---|---|---|---|---|---|
| 8.17% | 12.49% | 9.47% | 5.13% | 9.31% | 4.22% |
6.2蒙特卡洛模拟
蒙特卡洛模拟是一种随机预测的方法，其基本思想是在给定的条件范围以内，按照一定的规则生成模拟现实数值的方法，对于根据蔬菜历史价格模拟现实的随机性有极大帮助。
首先，我们对往期的价格及销量数据做出如下处理：
$$
x_{0i} = \ \frac{\sum_{i}^{n}{V_{i} \times x_{i}}}{\sum_{i}^{n}V_{i}}
$$
其中，$X_{0i}$是该品类的加权价格，$V_{i}$是单品i的销量，$X_{i}$是单品i的价格，n是样本总数量。
由于蔬菜的价格与需求有明显的周期性，且容易受到偶然因素的影响，因此，对于成本的预测，通过提取出蔬菜品类内部的价格周期变化规律，搜寻到商品价格变化的基本参数，在给定的条件范围内进行蒙特卡罗模拟，进而得出商超计划的进价成本。
其中，通过选取往年6-7月的品类价格作为样本数据，计算出每周相同时间下的平均销售量、方差，接着对成本价格数据进行十次蒙特卡罗模拟，得出接下来一周的成本结果如下：
表6:未来一周成本预测结果表
| 日期 | 水生根茎类 | 花叶类 | 花菜类 | 茄类 | 辣椒类 | 食用菌 |
|---|---|---|---|---|---|---|
| 7.1 | 11.4453 | 4.5446 | 5.3175 | 3.9880 | 5.8118 | 6.1392 |
| 7.2 | 9.8536 | 3.8964 | 5.3796 | 3.8154 | 6.9836 | 6.0061 |
| 7.3 | 8.9951 | 3.9233 | 5.7777 | 3.8368 | 6.6145 | 5.8379 |
| 7.4 | 11.0171 | 4.0261 | 5.3327 | 4.2586 | 5.6197 | 6.3354 |
| 7.5 | 11.9799 | 4.2130 | 4.8747 | 4.1076 | 7.0923 | 6.3269 |
| 7.6 | 11.3685 | 4.0845 | 5.8860 | 3.6476 | 6.9743 | 6.2739 |
| 7.7 | 10.4693 | 3.9124 | 5.1095 | 3.6244 | 6.0574 | 6.4426 |
6.3定价与销量的关系
在分析定价与销量关系时我们联想到，在微观经济学的定价模型中，销量与产品的价格之间存在着负相关性，综合应用所学，这里可以假设销量与价格之间的关系如下：
$$
V_{i} = f\left( P_{i} \right) + u_{i}
$$
其中, $u_{i}$是与多种因素有关的偏差值。
然而在实际操作中，$u_{i}$的数值无法通过模型具体测量。为了模拟偶然因素对价格的估计，对于残差值$u_{i}$，我们使用蒙特卡洛模拟进行估计，样本数据同6.2。
对于每个品类，通过对附件表格的处理得到价格与销量之间的关系。对每个品类的价格与销量进行一元回归拟合，得到的结果如下：
| 品类 | 回归方程 |
|---|---|
| 水生根茎类 | $\hat{Y_1}= 60.5456 – 2.776 X_{1}\ $ |
| 花菜类 | $\hat{Y_2}= 62.2037 – 2.6555 X_{2}$ |
| … | … |
其中$ \hat{Y_i} $表示的是该品类的销量, $X_i$表示的是该品类的加权定价。通过回归拟合，最终得出了蔬菜销量与价格的关系（考虑了偶然因素），记作:
$$
V_{i} = g\left( P_{i} \right)
$$
6.4最佳的日补货策略与销量策略
为制定出使商超收益最大化的每日补货总量与定价决策，我们首先分析如何能够使得总利润达到最大，则有：
$$
MaxW = \sum_{i}^{}{(P_{i} - C_{i})}V_{i}
$$
代入拟合的回归结果和定价与要求的目标利润率的关系，得到目标如下：
$$
MaxW = \sum_{i}^{}{\left\lbrack h\left( C_{i},R_{i} \right) - C_{it} \right\rbrack\ g}\left\lbrack h\left( C_{i},R_{i} \right) \right\rbrack
$$
之前的蒙特卡洛模拟已经给出7月1日至7月7日的成本变动情况，因此收益即为目标利润率的函数。
对于给定的目标函数，得到未来一周目标利润率以及最佳的日补货策略与销售价格策略结果如下表：
表8:未来一周目标利润率
| 日期 | 水生根茎类 | 花叶类 | 花菜类 | 茄类 | 辣椒类 | 食用菌 |
|---|---|---|---|---|---|---|
| 7.1 | 1.5018 | 1.6688 | 1.8474 | 1.6933 | 1.2787 | 1.6744 |
| 7.2 | 1.3557 | 1.6769 | 1.8514 | 1.735 | 1.359 | 1.4666 |
| 7.3 | 1.5315 | 1.6675 | 1.7827 | 1.7854 | 1.2054 | 1.6579 |
| 7.4 | 1.6175 | 1.6147 | 1.7598 | 1.751 | 1.4173 | 1.5242 |
| 7.5 | 1.2377 | 1.6203 | 1.7856 | 1.7033 | 1.3084 | 1.274 |
| 7.6 | 1.553 | 1.6856 | 1.7052 | 1.7126 | 1.2195 | 1.5399 |
| 7.7 | 1.6131 | 1.5974 | 1.8292 | 1.6282 | 1.3693 | 1.7208 |
表9:未来一周六中品类加权平均定价
| 日期 | 水生根茎类 | 花叶类 | 花菜类 | 茄类 | 辣椒类 | 食用菌 |
|---|---|---|---|---|---|---|
| 7.1 | 17.19 | 7.58 | 9.82 | 6.75 | 7.43 | 10.28 |
| 7.2 | 13.36 | 6.53 | 9.96 | 6.62 | 9.49 | 8.81 |
| 7.3 | 13.78 | 6.54 | 10.30 | 6.85 | 7.97 | 9.68 |
| 7.4 | 17.82 | 6.50 | 9.38 | 7.46 | 7.96 | 9.66 |
| 7.5 | 14.83 | 6.83 | 8.70 | 7.00 | 9.28 | 8.06 |
| 7.6 | 17.66 | 6.88 | 10.04 | 6.25 | 8.51 | 9.66 |
| 7.7 | 16.89 | 6.25 | 9.35 | 5.90 | 8.29 | 11.09 |
表10:未来一周六种品类补货计划
| 日期 | 水生根茎类 | 花叶类 | 花菜类 | 茄类 | 辣椒类 | 食用菌 |
|---|---|---|---|---|---|---|
| 7.1 | 20.25193 | 159.8993 | 35.78358 | 29.95829 | 61.84878 | 42.37662 |
| 7.2 | 23.86121 | 158.7716 | 36.11333 | 29.8218 | 62.75043 | 40.90494 |
| 7.3 | 19.20786 | 155.5153 | 36.14801 | 30.14889 | 64.96153 | 41.90185 |
| 7.4 | 22.50906 | 161.636 | 37.76511 | 28.63927 | 67.1932 | 39.70624 |
| 7.5 | 21.64149 | 158.7092 | 35.18366 | 28.13378 | 61.92483 | 38.67885 |
| 7.6 | 19.8674 | 165.5781 | 34.8044 | 32.46147 | 58.29738 | 39.65557 |
| 7.7 | 17.83155 | 154.8491 | 37.29228 | 29.06026 | 61.54267 | 36.68715 |
七、 问题三模型的建立与求解
7.1与问题二的区别与联系
问题三与问题二之间存在着紧密的联系，两者都要求制定补货与定价策略，使得商超收益最大。区别在于问题三的限制更多，例如对单品总数及订购量均存在要求，同时问题三还强调商超收益最大化要在满足市场对各品类蔬菜商品需求的前提下。考虑到诸多限制条件，故问题三更适合采用多约束目标规划的方法进行解决。同时，在问题二中，需要考虑的样本数据可以是每一年同一时间段的商品销售数据，而在问题三中，参考的样品数据则限制到前一周（2023.06.23-2023.06.30），这就要求根据数据情况采用更合适的预测方法。
7.2目标函数的确立
因此，与问题二的规划问题不同，问题三可以看作是一个多约束的整数规划问题。我们设定目标函数值为各单品利润总和，函数的具体表达如下：
$$
MaxW = \sum_{i}^{}\left( p_{i} - c_{i} \right)S_{i}n_{i}(1 - \rho_{i})
$$
其中，$n_{i}$表示是否购买第i种单品，若是则$n_{i}$的值为1，反之则为0。$\rho_{i}$表示的是第i种商品的损耗率。我们统计了2023.06.23-2023.06.30销售过的单品种类，共计49种，由于单品总数存在上限，故只考虑对该49种单品进行规划。
对于成本$c_{i}$，由于一周内同一单品成本变动较小，故可以使用指数平滑法对7月1日各单品的成本进行预测。指数平滑法的核心是赋予较近期的观测值更高的权重，以便更好地捕捉数据的变化趋势。流程如下：
| 指数平滑法流程 |
|---|
| ①初始化：选择一个平滑参数$\ \alpha\ $= 0.5，以及初始数据点 |
| ②预测下一个时间点的值: 假设当前时间点为t，其估计值为$Y_{t}$，下一个时间点为 $t+1$，观测值为$ X_{t} + 1 $ |
| ③则预测下一个时间点的值为： $Y_{t} + 1=\alpha X_{t} + 1 + (1 - \alpha )Y_{t}$ |
| ④更新估计值：将新的估计值 $ {(Y}_{t} + 1) $ 用于预测下一个时间点，然后重复步骤2，逐步预测未来的单品成本。 |
通过对数据的预处理和观察分析发现：在商品的单价、成本、销售量等各项指标中，销售量的变动程度是最剧烈的，因此若是仅仅使用过去的销售量对未来的销售量进行预测，恐怕难以保证其准确性。因此，我们考虑从概率分布的角度对市场需求进行度量。具体而言，我们假设市场需求服从正态分布，根据2023年6月24-30日各单品的销售量对市场需求进行刻画。使用计算得到的销售量均值与方差刻画市场需求的均值与方差，记为$\mu$和$\sigma^{2}$，则市场需求量$ X\thicksim N\left. （\mu,\sigma^{2} \right.）$，其概率密度函数为：
$$
f(x) = \frac{1}{\sqrt{2 \pi } \sigma} \exp\left\lbrack - \frac{ {(x - \mu) }^{2} }{2\sigma^{2}} \right\rbrack
$$
接下来我们将分析销售量与补货量之间的关系。在我们的模型中，并没有将销售量与补货量视为相等的变量，因为补货量反映了商家对于未来市场需求的判断，而销售量则反映了真实的市场需求。当市场需求较少时，销售量为市场的需求量；而当市场需求较大时，销售量则是商家的补货量。记销售量为$S_{i}$，补货量为$T_{i}$，市场需求量为$X_{i}$ 则有：
$$
S_{i} = \min(T_{i},X_{i})
$$
而市场需求量为$X_{i}$服从正态分布，故可使用概率密度积分的方法对销售量$S_{i}$进行估计，具体如下式：
$$
S_{i} = \int_{- \infty}^{T_{i} }{xf(x)}dx + T_{i}\int_{T_{i} }^{\infty}{f(x)}dx
$$
于是我们便得到了销售量$S_{i}$关于补货量$T_{i}$的函数。
接下来我们将分析商品价格$P_{i}$与市场需求量$X_{i}$的关系。已知市场需求量$X_{i}$的分布由均值$\mu$与方差$\sigma^{2}$决定，而我们的模型认为：商品$i$需求量的方差由商品$i$自身的属性决定，不会受到价格等外在因素的影响，故商品价格$P_{i}$对市场需求量$X_{i}$的影响主要体现在均值$\mu$上。考虑使用2023.06.23-2023.06.30的价格与销售量数据进行如下线性回归：
$$
\mu_{i} = \alpha_{i}\ P_{i} + \beta_{i}
$$
至此，目标函数的转化告一段落，接下来是对约束条件的分析。
7.3约束条件
7.3.1商超的最大进货量
最大容量是最大进货量的限制条件。用销售量代替进货量，找到前两年中最多的日销售量，该销售量即为最大进货量。本周的进货条件需要满足：
$$
n_i x_i < S_{\max}，i = 1,2,\ldots,49
$$
其中，$S_{max}$是商超在所有时期内的单日总进货量的最大值。
7.2.2商超的最小进货量
商超的最小进货量需要保证对商品品类最小的需求。考虑上一周的进货量数据，某一品类的最小进货量需要满足上一周内的最小需求量数据，即：
$$
n_i t_i < S_{jmin}，i = 1,2,\ldots,49
$$
其中，$S_{j\min}$是品类j在上一周内的销售量最小值。
7.2.3商超订货种类的限制
由题意可知：
$$
27 \leq \sum_{i = 1}^{49}n_{i} \leq 33
$$
故商超订货种类的限制为27至33种。
7.2.4对单种商品进货数量的最小限制
任意进货商品的销售量需要大于2.5千克。
但商品不再进货时，则有$t_{i} > 2.5，i = 1,2,\ldots,49$
7.2.5商超需要满足市场对各品类蔬菜商品的需求。
同品类蔬菜进货量之和大于等于过去一周对应品类日销量的均值
$$
\sum_{i=1}^{49} T_i \geq Aver_j , j = 1,2,\ldots,6, Type_i=j
$$
$Type_i$为第i个单品所属品类，$Aver_j$为过去一周第j品类蔬菜日销量的均值。
7.3结论
最终，我们得到如下目标规划：
$$
MaxW = \sum_{i = 1}^{49}\left( p_{i} - c_{i} \right)\left\lbrack \int_{- \infty}^{T_{i}}{xf(x)}dx + T_{i}\int_{T_{i}}^{\infty}{f(x)}dx \right\rbrack n_{i}(1 - \rho_{i})
$$
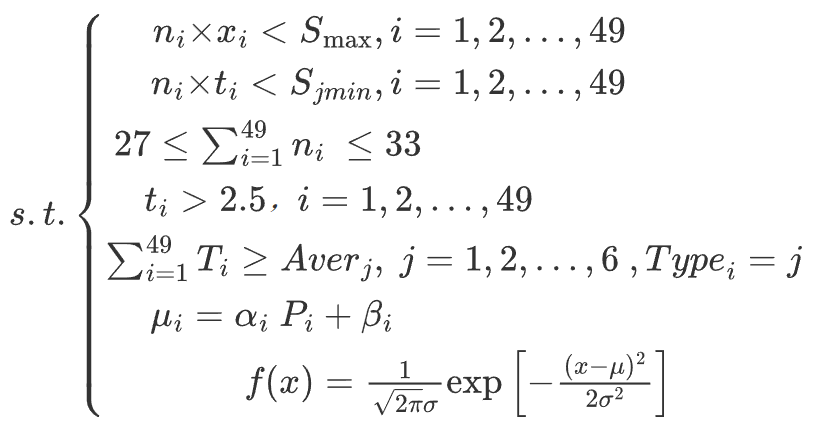
我们使用MATLAB编写代码对上述目标规划进行求解，确定采购单品种类为33种，其补货量及定价如下表所示：
| 单品名称 | 补货量（千克） | 定价（元/千克） |
|---|---|---|
| 上海青 | 3.86 | 8.00 |
| 云南油麦菜 | 1.70 | 7.20 |
| 云南生菜(份) | 32.29 | 4.37 |
| 净藕(1) | 6.03 | 14.34 |
| 双孢菇(盒) | 10.00 | 5.03 |
| 奶白菜 | 7.49 | 4.80 |
| 姜蒜小米椒组合装(小份) | 7.00 | 4.68 |
| 娃娃菜 | 10.43 | 6.50 |
| 小皱皮(份) | 11.29 | 2.57 |
| 小米椒(份) | 21.43 | 5.77 |
| 小青菜(1) | 4.90 | 5.20 |
| 木耳菜 | 5.93 | 5.46 |
| 洪湖藕带 | 4.03 | 20.99 |
| 海鲜菇(包) | 8.86 | 2.72 |
| 竹叶菜 | 13.30 | 3.74 |
| 紫茄子(2) | 10.90 | 6.00 |
| 红椒(2) | 2.04 | 18.84 |
| 红莲藕带 | 0.66 | 9.20 |
| 红薯尖 | 4.51 | 5.37 |
| 芜湖青椒(1) | 14.23 | 5.20 |
| 苋菜 | 8.92 | 3.74 |
| 菠菜(份) | 9.80 | 5.33 |
| 菱角 | 2.04 | 14.00 |
| 虫草花(份) | 2.29 | 3.37 |
| 螺丝椒 | 6.84 | 11.43 |
| 螺丝椒(份) | 11.29 | 4.96 |
| 西兰花 | 12.56 | 12.63 |
| 西峡花菇(1) | 4.62 | 24.00 |
| 金针菇(盒) | 16.14 | 1.86 |
| 长线茄 | 4.21 | 12.00 |
| 青红杭椒组合装(份) | 2.14 | 5.31 |
| 青茄子(1) | 3.12 | 6.00 |
| 高瓜(1) | 3.00 | 13.52 |
八、 问题四模型的建立与求解
8.1影响蔬菜的补货与定价因素的探讨
8.1.1供应商的质量与数量。
由题意知，商超所出售的产品种类达到250余种。据此，可供商超选择的供应商不一定只有一家。当存在多家供应商和多家运货商时，对商家的更合理的选择也是减少成本，增加总利润的方法之一。
8.1.2运货商的质量与数量
当总的进货量超过了一家运货商的运输限制时，或者是一家运货商无法从多个产地运输蔬菜时，商超需要选择多家运货商。超市需要选择质量高的运货商，减少蔬菜的损耗，还要尽可能减少运货商的数量，减少固定成本。
8.1.3超市内人员的数量
销量上限会随着人员数量的变化而变化。当人手数量不足时，即使需求量再大，销量也是有限的。然而增加人手会导致固定成本的增加，因此最佳的人手数量也是需要考虑的因素之一。
8.2定性讨论蔬菜的补货与定价因素的探讨
在问题三中，我们得到了收益的目标函数，即：
$$
MaxW = \sum_{i}^{}\left( p_{i} - c_{i} \right)S_{i}n_{i}(1 - \rho_{i})
$$
当考虑如上因素时，对目标函数和约束条件做出如下调整：
8.2.1考虑供应商的情况
假设第t家供货商的订货价格为$M_{1t}$，第t家供货商的最大供货量为$X_{1mt}$，则目标函数调整为：
$$
MaxW = \sum_{i}^{}\left( p_{i} - c_{i} \right)S_{i}n_{i}(1 - \rho_{i})S_{i} - \sum_{t}^{}M_{1t}
$$
为了保证供货量，新增约束条件为：
$$
\sum_{t}^{}X_{1m} \geq \sum_{i}^{}X_{i}
$$
8.2.2考虑转运商的情况
假设第t家运货商的订货价格为$M_{2t}$，第t家转运商的最大供货量为$X_{2mt}$，则目标函数调整为，第t家商家转运的损耗率为$Q_{t}$，则目标函数调整为：
$$
MaxW = \sum_{t}^{}{\sum_{i}^{}\left( p_{i} - c_{i} \right)S_{i}n_{i}\left( 1 - \rho_{i} \right)\left( 1 - Q_{t} \right)} - \sum_{t}^{}M_{2t}
$$
为了保证运货量，新增约束条件为：
$$
\sum_{t}^{}X_{2m} \geq \sum_{i}^{}X_{i}
$$
8.2.3考虑超市内人员安排的情况
由于不同员工会为超市带来不同的种类的效益，衡量方法不同，这里不再赘述。
九、模型的评价
9.1.模型的优点分析
1.充分考虑了数据特点，对大量的数据进行了合理的简化操作，便利了后续的优化操作。
2.本文采取正太分布的蒙特卡罗模拟方法，且多次模拟，使得拟合出的数据更加贴近真实情况。
3.充分考虑根据拟合回归的情况，根据拟合优度的可靠性做出数据的取舍，避免了相关性低的数据对拟合结果的干扰。
4.对于每个可能对目标函数或结果造成影响的部分，都严格给出了数学公式定性说明影响情况，说服力充分。
5.聚类分析减少数据的复杂度，通过对聚类特征的描述取代对单品数据的描述，简化了问题，为合理操作。
9.2模型的缺点分析
1.在对数据的处理过程中，将占比较低的退货数据和打折销售数据做了剔除的处理。这样做简化了数据更便于操作，但也一定程度上降低了数据与真实情况的相似程度。
2.本文只考虑了多元数据间线性拟合的情况，实际上多数据之间的关系不一定仅是线性的，其间可能存在高次或者是其它较为复杂的函数关系。
9.3模型的改进方案
1.分类考虑的退换货以及折扣的情况，对更多更复杂的情况进行模拟。
2.将拟合的模型从多元线性拟合变更为多元高次拟合或者是多元高斯拟合等其它拟合模型。
十、参考文献
[1]冷建飞,高旭,朱嘉平.多元线性回归统计预测模型的应用[J].统计与决策,2016(07):82-85.DOI:10.13546/j.cnki.tjyjc.2016.07.021.
[2]金辉,陶兰.基于蒙特卡罗模拟的新三板信息技术企业价值评估[J].中国资产评估,2016(09):22-28.
[3]杨俊闯,赵超.K-Means聚类算法研究综述[J].计算机工程与应用,2019,55(23):7-14+63.
[4]曾贺奇,张玉林.考虑消费者策略行为及产品具有替代性的多厂商定价[J].系统工程,2017,35(01):130-137.
求求富哥打赏~QwQ
