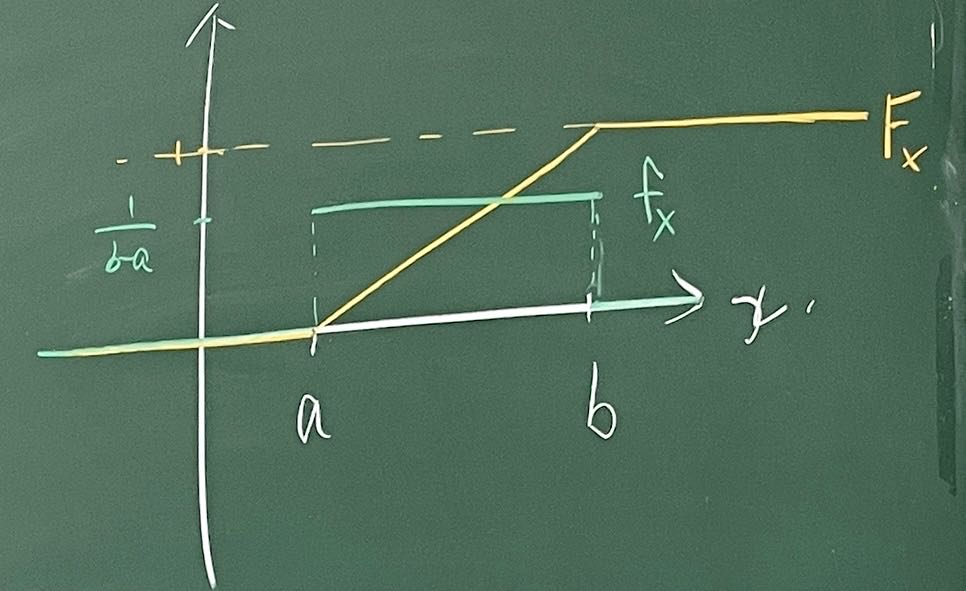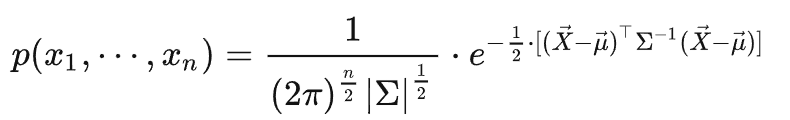随机变量的类型
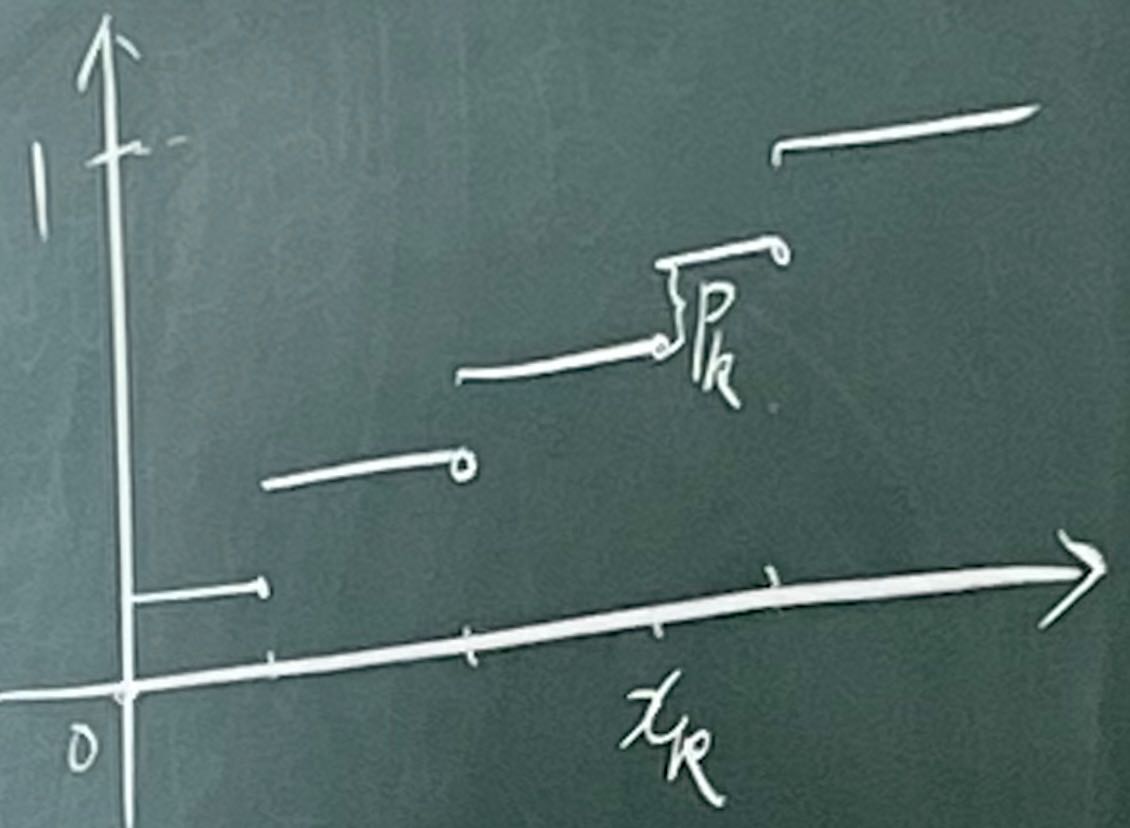
离散型随机变量
离散型随机变量的分布函数不连续,至多有可数个间断点(跳跃型间断点)
FX(x)=k:xk≤x∑P(X=xk)=k:xk≤x∑Pk(1)
0≤Pk≤1k=1∑∞Pk=1
我们称满足(1)式的分布函数及相应的随机变量为离散型。
例1:
二项分布$ B(n,p)$
Pk=P(X=k)=Cnkpk(1−p)n−kk=0,1,2,...n
伯努利分布(Bernoulli):n=1 的二项分布
二项分布是多次伯努利分布。
例2
参数为λ的泊松Poisson分布 P(λ)
Pk=P(X=k)=k!λke−λ
其中 k=0,1,2,3...
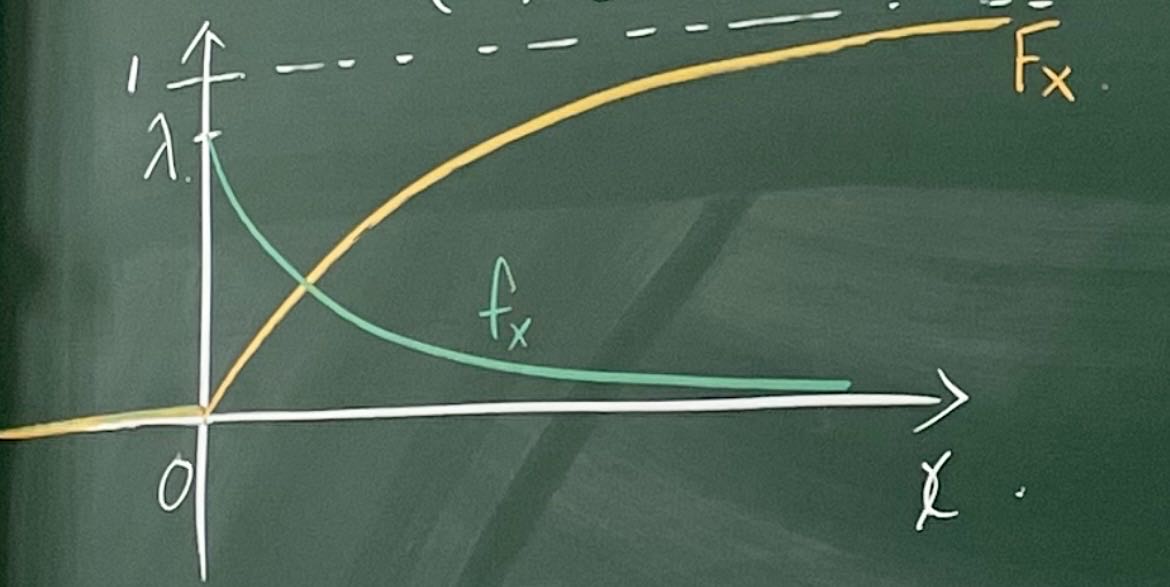
连续型随机变量
若分布函数连续,则 r.v.X 称为连续型随机变量,则:
∀x∈R,P(X=x)=0
大多数连续型r.v.都有密度函数:
fX(x) x∈R
使得:
FX(x)=∫−∞xfx(y)dyFx′=fx
其中:
fx≥0∫−∞∞fX(y) dy=1
例1
均匀分布 U(a,b) (Uniformly distribution)
FX(x)=⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧0,x≤ab−ax−a,a<x<b1,x≥b
fX(x)=⎩⎪⎪⎨⎪⎪⎧b−a1,x∈(a,b)0,x∈/(a,b)
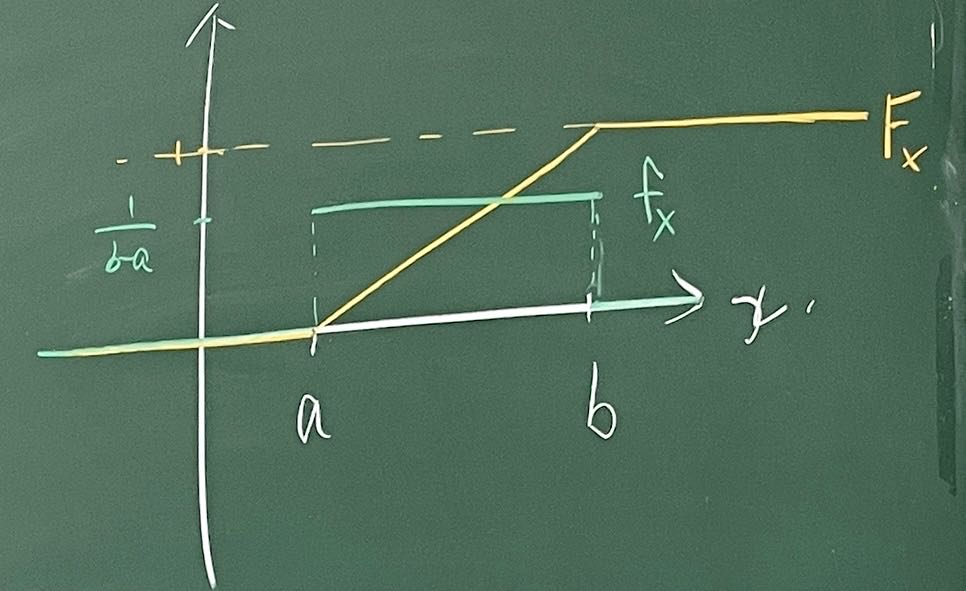
如何理解均匀分布:
并非每个点概率都一样就是均匀分布,因为任何连续型分布每个点概率均为零。
正确理解为:在(a,b)上取定长区间,概率相等。
例2
参数为λ的指数分布
FX(x)=⎩⎪⎪⎨⎪⎪⎧ 0 ,x<0 1−e−λx,x≥0
fX(x)=⎩⎪⎨⎪⎧0x<0λe−λxx≥0
例3
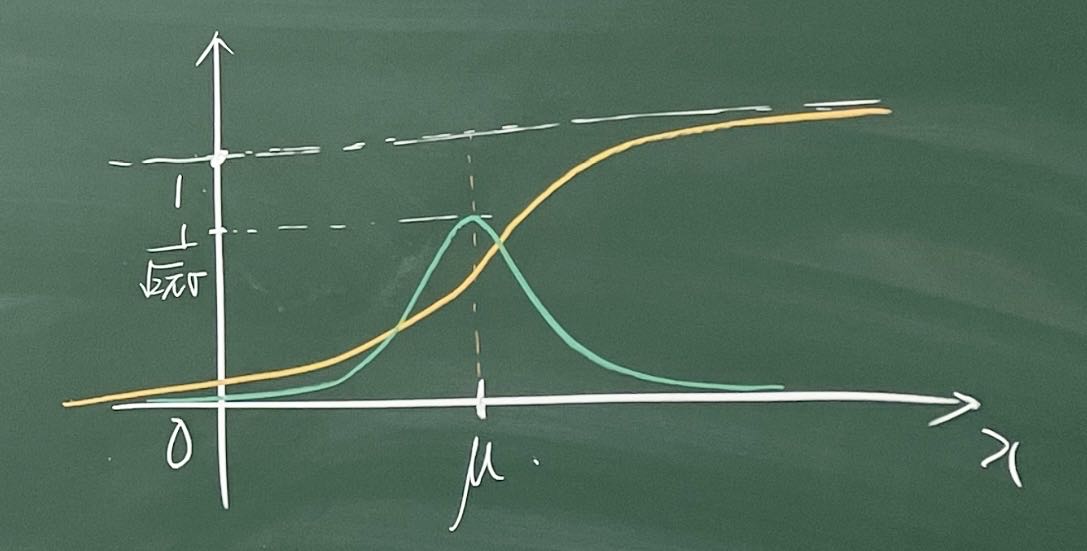
正态分布 N(μ,σ2) Normal Distribution
∀x∈R fX(x)=2πσ1e2σ2(x−μ)2
FX(x)=∫−∞xfX(y) dy
若μ=0,σ=1 ,则为标准正态分布 N(0,1)
既不离散,又不连续,如:
X∼P(λ)Y∼N(0,1)Z=X+Y
中心极限定理:对于独立并同样分布的随机变量,即使原始变量本身不是正态分布,标准化样本均值的抽样分布也趋向于标准正态分布
数学期望、方差、矩
1、连续型r.v.X有密度函数fx
数学期望:
μX=E[X]=∫−∞∞xfX(x) dx
方差:
σX2=Var(X)=E[(X−μX)2]=E[X2]−μX2=∫−∞∞(x−μX2)fX(x) dx
标准差:
σX=Var(X)
l 阶距:
E[Xl]=∫−∞∞xlfX(x) dx
∀ 函数g , Y=g(x) 的期望:
E[Y]=E[g(X)]=∫−∞∞g(x)fX(x) dx
易错注意:E[g(x)]=g(E(x))
2、离散型r.v.X 设P(X=xk)=Pk
数学期望:
μX=E[X]=k∑xkPk
方差:
σX2=Var(X)=k∑(xk−μk)2Pk
标准差:
σX=Var(X)
l 阶距:
E[Xl]=k∑xklPk
g(X) 的期望:
E[g(X)]=k∑g(xk)Pk
从样本空间到实数域:
E[X]=∫ΩX(ω) dP(w)=∫Rx dFX(x)
定理1: 切比雪夫不等式 (chebyshev)
r.v.X E[X]=μ Var(X)=σ2
则:
∀ε>0 P( ∣X−μ∣≥ε)≤ε2σ2
含义:随机变量X落在数学期望E(X)的领域内的概率是很大的
证明:
首先我们定义示性函数 IA:
IA(ω)={0 ,ω∈/A1 ,ω∈A ∀ω∈Ω
E[IA]=1∗P(A)+0∗(1−P(A))=P(A)
P( ∣X−μ∣≥ε)=E[ I∣X−μ∣≥ε ]=E[ I∣X−μ∣2≥ε2 ]
因为 I∣X−μ∣2≥ε2 只能取0 或 1,若I=0 ,则$0<\frac{|X-\mu|^2}{\varepsilon^2} <1 $ ;若I=1,则$\frac{|X-\mu|^2}{\varepsilon^2} \geq 1 $
故:
I∣X−μ∣2≥ε2≤ε2∣X−μ∣2
两边同时取期望:
E[I∣X−μ∣2≥ε2]≤E[ε2∣X−μ∣2]=ε2σ2
得证。
随机向量
若 X=(X1,X2,...,Xn) ,其中 $ \forall i$ ,Xi 是一维随机变量,则 X 称为 n 维随机向量(Random vector) (r.v.)
分布函数
FX(x)=P(X1≤x1, X2≤x2, ..., Xn≤xn)=P({ω:X1(ω)≤x1, X2(ω)≤x2, ..., Xn(ω)≤xn})
其中:
X=(X1,X2,...,Xn) , x=(x1,x2,...xn)∈R
∀B∈B (n维度Borel代数)PX(B)=P({ω:Xi(ω)∈B})=P(X∈B)
称为随机向量X的分布
概率密度
若随机变量 X=(X1,X2,...,Xn) 有密度 fx ,则分布函数 FX(x) 可以表示为
FX(x)=∫−∞x1∫−∞x2...∫−∞xnfX(y1,y2,...yn)dyn...dy2dy1
x=(x1,x2,...,xn)∈Rn , fx≥0
且:
∫−∞∞∫−∞∞...∫−∞∞fX(y1,y2,...yn)dyn...dy2dy1=1
边缘密度及分布函数
略。
数学期望
E[X]=(E[X1],E[X2],...,E[Xn])
协方差矩阵
x∑=(σij)n∗n
是一个对称矩阵,其中:
σij=cov(Xi,Xj)=E[(Xi−E[Xi])(Xj−E[Xj])]=E[XiXj]−E[Xi]E[Xj]
是Xi和Xj的协方差,1≤i≤n,1≤j≤n
可证明∑x是一个半正定矩阵。
证明:
正定矩阵(positivedefinite):给定一个大小为n∗n 的实对称矩阵 A ,若对于任意长度为n的非零向量x,有xTAx>0恒成立,则矩阵A是一个正定矩阵。
半正定矩阵(positivesemi−definite):给定一个大小为n∗n 的实对称矩阵 A ,若对于任意长度为n的非零向量x,有xTAx≥0恒成立,则矩阵A是一个半正定矩阵。

例*:n维高斯(随机)向量 ( n维正态向量)
X=(X1,X2,...Xn)
密度函数:
∀x=(x1,x2,...,xn)∈Rn
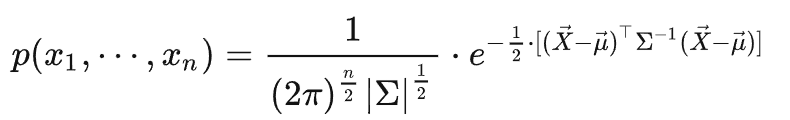
其中:
μ=(μ1,μ2,...,μn) :数学期望
∑:X的协方差矩阵det∑:∑的行列式(∑)−1:∑的逆矩阵
二维:
∑=(σ12σ1σ2σ1σ2σ22)
X和Y的相关系数:
ρXY=Var(X) Var(Y)Cov(X,Y)
性质:
对n维高斯向量作线性变换,得到的仍是高斯向量。
X=(X1,X2,...Xn)∼N(μ,∑)
设A为m∗n的矩阵
AX∼N(Aμ,A∑AT)
(AX 是一个m维的高斯向量)
*二维高斯随机向量的密度图形:横截面是椭圆
*密度函数指数部分对应着椭圆