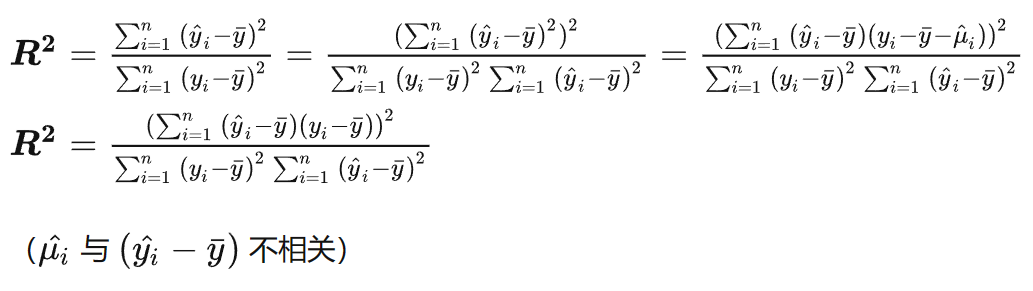多元回归模型

$$
y=\beta_0+\beta_1x_1+\beta_2x_2+…+\beta_kx_k+u
$$

Example：

可以在模型中加入更多的解释变量：
$$
wage=\beta_0+\beta_1educ+\beta_2{exper}+u
$$
更加灵活的方程形式：

家庭收入（inc）和消费（cons）的关系：
$$
cons=\beta_0+\beta_1inc+\beta_2inc^2+u
$$

多元回归方程的推导

总体方程：
$$
y_i=\beta_0+\beta_1x_{i1}+\beta_2x_{i2}+…+\beta_kx_{ik}+u_i
$$
拟合值：
$$
\hat{y_i}=\hat{\beta_0}+\hat{\beta_1}x_{i1}+\hat{\beta_2}x_{i2}+…+\hat{\beta_k}x_{ik}
$$
残差：
$$
\hat{u_i}=y_i-\hat{y_i}=y_i-\hat{\beta_0}-\hat{\beta_1}x_{i1}-\hat{\beta_2}x_{i2}-…-\hat{\beta_k}x_{ik}
$$
最小化残差平方和：
$$
min\sum_{i=1}^n \hat{u_i}^2=min\sum_{i=1}^n(y_i-\hat{\beta_0}-\hat{\beta_1}x_{i1}-\hat{\beta_2}x_{i2}-…-\hat{\beta_k}x_{ik})^2
$$
一阶条件（分别对$\beta_i$求导）：
$$
\frac{\partial \sum_{i=1}^n \hat{u_i}^2}{\partial \hat{\beta_0}}=\sum_{i=1}^n-2(y_i-\hat{\beta_0}-\hat{\beta_1}x_{i1}-\hat{\beta_2}x_{i2}-…-\hat{\beta_k}x_{ik}) =\sum_{i=1}^n \hat{u_i}=0
$$

$$
\frac{\partial \sum_{i=1}^n \hat{u_i}^2}{\partial \hat{\beta_1}}=\sum_{i=1}^n-2x_{i1}(y_i-\hat{\beta_0}-\hat{\beta_1}x_{i1}-\hat{\beta_2}x_{i2}-…-\hat{\beta_k}x_{ik}) =\sum_{i=1}^n x_{i1}\hat{u_i}=0
$$

同理对于$ \forall k>0$：
$$
\sum_{i=1}^n x_{ik}\hat{u_i}=0
$$
k+1个方程求解k+1个变量。

数值特征：

样本均值点在回归线上

$$
\bar{y}=\hat{\beta_0}+\hat{\beta_1}\bar{x}_1+\hat{\beta_2}\bar{x}_2+…+\hat{\beta_k}\bar{x}_k
$$

证明：
$$
\sum_{i=1}^n\hat{u_i}=\sum_{i=1}^n(y_i-\hat{y_i})=0 \
=> \ \ \bar{y}=\bar{\hat{y}}
$$
再对n个估计式累加再除以n，易得证。

每个自变量和OLS残差之间的样本协方差为零

样本协方差为：
$$
=\frac{1}{n-1}(\sum_{i=1}^n(x_{i1}-\bar{x})(\hat{u_i}-\bar{\hat{u}})) \
=\frac{1}{n-1}(\sum_{i=1}^n x_{i1}\hat{u_i}-\sum_{i=1}^n x_{i1}\bar{\hat{u}}-\sum_{i=1}^n \bar{x}\hat{u_i}+\sum_{i=1}^n \bar{x}\bar{\hat{u}}) =0
$$

*高级计量结果

$$
\hat{\beta}=(X’X)^{-1}X’y
$$

对多元回归排除其他变量的解释

字面上来说，$\beta_i$是保持其他变量不变时，$x_i$变化对$y$的影响。而事实上，自变量之间存在或多或少的关联，如$x_1$的变动会导致$x_2$的变动，而$x_2$的变动又会导致$y$的变动。但我们在衡量$x_1$对$y$的影响(即$\beta_1$)时仅仅考虑$x_1$对$y$的直接影响，通过其他变量间接传导的影响不在考虑之内。

正因如此，多元回归的系数结果通常不等于一元回归，因为多元回归中自变量大概率存在关联性，而多元回归的过程中自动排除了相关变量间接传导的影响。

$\hat{\beta_1}$可以写成另外一个形式：
$$
\hat{\beta_1}=\frac{\sum_{i=1}^n\hat{r}{i1}y_i}{\sum{i=1}^n\hat{r}_{i1}^2}
$$
其中，残差$r$来自$x_1$对$x_2,x_3,…,x_k$的回归。

证明：

已知 $x_{i1}=\hat{x}{i1}+\hat{r}{i1}$，代入原回归的一阶条件得：
$$
\sum_{i=1}^n (\hat{x}{i1}+\hat{r}{i1})(y_i-\hat{\beta}0-\hat\beta_1x{i1}-…-\hat{\beta}kx{ik})=0
$$
而$\hat{x}{i1}$是$x{i2},…,x_{ik}$的线性函数，故 $\sum_{i=1}^n\hat{x}{i1}\hat{u}i=0$，于是：
$$
\sum{i=1}^n \hat{r}{i1}(y_i-\hat{\beta}0-\hat\beta_1x{i1}-…-\hat{\beta}kx{ik})=0
$$

而 $\hat{r}{i1}$是残差，故$\sum{i=1}^n x_{ij}\hat{r}{i1}=0$，于是：
$$
\sum{i=1}^n \hat{r}{i1}(y_i-\hat\beta_1x{i1})=0 \
\sum_{i=1}^n \hat{r}{i1}(y_i-\hat\beta_1(\hat{x}{i1}-\hat{r}{i1}))=0 \
\sum{i=1}^n \hat{r}{i1}(y_i-\hat\beta_1\hat{r}{i1})=0
$$
最终得到：
$$
\hat{\beta_1}=\frac{\sum_{i=1}^n\hat{r}{i1}y_i}{\sum{i=1}^n\hat{r}_{i1}^2}
$$

理解:

因为残差$\hat{r}{i1}$是$x{i1}$中与剩余$x_{j1}$不相关的部分，故$\hat{\beta}_1$度量了排除其他自变量影响后$y$与$x_1$的关系。这个结果成为弗里施-沃定理（$Frish-Waugh \ theorem$），这种回归方式称为分块回归或偏回归。

拟合优度$R^2$

$R^2$等于$y_i$实际值与其拟合值$\hat{y_i}$的相关系数的平方
$$
R^2=(corr(y_i,\hat{y_i}))^2=\frac{(\sum_{i=1}^n(y_i-\bar{y})(\hat{y_i}-\bar{\hat{y}}))^2}{(\sum_{i=1}^n(y_i-\bar{y})^2)(\sum_{i=1}^n(\hat{y_i}-\bar{\hat{y}})^2)}
$$
证明：

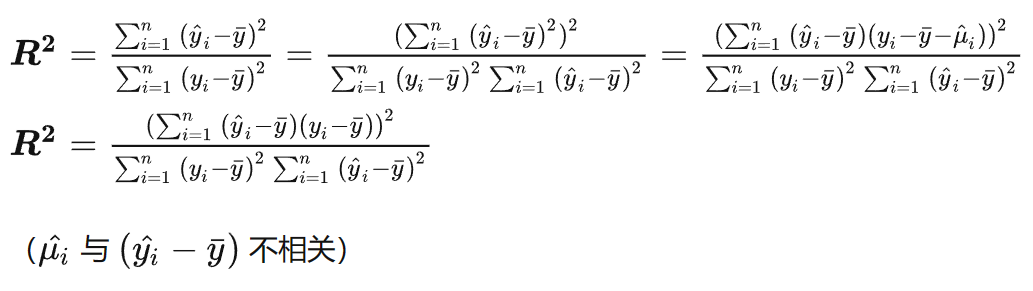
$OLS$估计量的期望值

经典假设条件

Assumption MLR.1 (线性于参数)

$$
y=\beta_0+\beta_1x_1+\beta_2x_2+…+\beta_kx_k+u
$$

这是对总体模型或真实模型的规范表述

Assumption MLR.2 (随机抽样)

$$
{ (x_{i1},x_{i2},…,x_{ik},y_i): i = 1…n }
$$

$$
y_i=\beta_0+\beta_1x_{i1}+\beta_2x_{i2}+…+\beta_kx_{ik}+u_i
$$

该假设控制了单个样本不受其它样本影响。

Assumption MLR.3 (No perfect collinearity不存在完全共线性)

在样本中，没有一个自变量是常数，自变量之间也不存在严格的线性关系（可以有相关性）。

从矩阵来看，如果存在线性关系，就不满秩了，也就没有逆矩阵了。

该假设可以保证存在唯一的$OLS$估计值

Assumption MLR.4(条件均值为零)

$$
E(u_i|x_{i1},x_{i2},…,x_{ik})=0
$$

简单来说，误差项和解释变量是不相关的。

具体意味着，影响$y$的其他因素总体上与$x_{i1},x_{i2},…,x_{ik}$不相关。

定理3.1 无偏性

由$MLR.1-MLR.4$可以推导出：
$$
E(\hat{\beta_j})=\beta_j
$$

初等代数证明：

我们已知：
$$
\hat{\beta_1}=\frac{\sum_{i=1}^n\hat{r}{i1}y_i}{\sum{i=1}^n\hat{r}{i1}^2}
$$
将总体方程代入：
$$
y_i=\beta_0+\beta_1x{i1}+\beta_2x_{i2}+…+\beta_kx_{ik}+u_i
$$
可得：
$$
\hat{\beta_1}=\beta_1+\frac{\sum_{i=1}^n\hat{r}{i1}u_i}{\sum{i=1}^n\hat{r}{i1}^2}
$$
考虑到$\hat{r}{i1}$只是样本自变量的函数，于是：
$$
E(\hat{\beta}1|X)=\beta_1+\frac{\sum{i=1}^n\hat{r}{i1}E(u_i|X)}{\sum{i=1}^n\hat{r}_{i1}^2}=0
$$
得证。

矩阵证明：

​ 暂时略，后续补充。

实证研究中，有些情况可能会影响我们获得无偏估计值，如：

哪些情况会影响我们获得无偏估计值？

遗漏变量：

假设真实世界中：
$$
y=\beta_0+\beta_1x_1+\beta_2x_2+u
$$
但由于种种因素，导致我们忽略了$x_2$的存在，仅以为：
$$
y=\alpha_0+\alpha_1x_1+w
$$
$x_2$某种程度上变成了$w$的一部分。

而$x_2$与$x_1$之间存在关系:
$$
x_2=\delta_0+\delta_1x_1+v
$$
则：
$$
y=\beta_0+\beta_1x_1+\beta_2(\delta_0+\delta_1x_1+v)+u \
=(\beta_0+\beta_2\delta_0)+(\beta_1+\beta_2\delta_1)x_1+(\beta_2v+u)
$$
这导致我们的估计值为：
$$
\alpha_1=\beta_1+\beta_2\delta_1
$$
与真实结果产生了偏差。而估计值由两部分构成，一部分是$x_1$本身的影响，另一部分是$x_1$通过影响$x_2$间接对$y$产生的影响。

如果结果不产生偏差，则说明：
$$
\delta_1 =0 \ \ \ 或 \ \ \ \beta_2=0
$$
即，要么样本中$x_1$和$x_2$不相关，要么$x_2$本身对$y$没有影响。

在回归模型中加入自变量的过程某种程度上可以理解为不断控制变量的过程，例如，在衡量$x_1$的影响时，模型自动排除了$x_2,x_3…x_n$的影响。

如果$x_2$只与$y$有关而与$x_1$无关，则不会的$\beta_1$的无偏性造成影响，只是由于遗漏$x_2$导致误差项中的$\sigma^2$提升，进而会提高$Var(\beta_1)$。（当然$R_j^2$也会有所变化，但因为$x_2$与$x_1$无关，所以$R_j^2$变化不大）因此，一般认为$x_2$也要加入回归。

$OLS$统计量的方差

Assumption MLR.5 (同方差性)

$$
Var(u_i|x_{i1},x_{i2},…,x_{ik}) = \sigma^2
$$

给定任意解释变量值，误差$u$都具有相同的方差。

由$MLR.5$：
$$
Var(y|X)=\sigma^2
$$
即给定$x$，$y$的方差不取决于自变量的值。

定理3.2 $OLS$斜率估计量的抽样方差

根据假设$MLR.1-MLR.5$（高斯-马尔科夫假定），可以推导到：
$$
Var(\hat{\beta_j})=\frac{\sigma^2}{SST_j(1-R_j^2)} \ \ \ \ \ ,j=1,2…k
$$
其中：
$$
SST_j=\sum_{i=1}^n(x_{ij}-\bar{x}_j)^2
$$
$SST_j$用来衡量自变量$x_j$的样本波动性

$R_j^2$是一个拟合优度，来自一个回归模型，其中因变量为$x_j$，自变量是其他解释变量（包括常数项），其本质上是在衡量其他$x$与$x_j$的相关程度。
$$
x_j=\alpha_0+\alpha_1x_1+…+\alpha_{j-1}x_{j-1}+\alpha_{j+1}x_{j+1}+…+\alpha_kx_k+v
$$

证明

$$
Var(\hat{\beta_1})=Var(\frac{\sum_{i=1}^n\hat{r}{i1}y_i}{\sum{i=1}^n\hat{r}{i1}^2}) =\frac{\sum{i=1}^n\hat{r}{i1}^2Var(u_i|X)}{(\sum{i=1}^n\hat{r}{i1}^2)^2}
=\frac{\sum{i=1}^n\hat{r}{i1}^2\sigma^2}{(\sum{i=1}^n\hat{r}{i1}^2)^2}
=\frac{\sigma^2}{\sum{i=1}^n\hat{r}_{i1}^2}
$$

因为$\sum_{i=1}^n\hat{r}^2_{i1}$是$x_1$对$x_2,…,x_k$回归的残差平方和，故：
$$
\sum_{i=1}^n\hat{r}^2_{i1} =SST_1(1-R_1^2)
$$
得证。

从上述公式来看，$Var(\hat{\beta_j})$受三个部分影响。

  • $\sigma^2$越大，方差中“噪声”越大，导致方差越大

  • $x_j$的总样本波动越大，跨度越大，结果越准确，$\beta$的方差就越小

  • 如果$R^2$很大，代表着相关性很大，代表着很多信息由于相关性而产生了重叠，“有用”的信息越少，方差越大。

多重共线性

两个或多个自变量之间高度（但不完全）相关被称为多重共线性$(multicollinearity)$

解决多重共线性的方法

1、把一些变量加总起来（如各项支出）

2、把某些变量剔除（装看不见嘿嘿），尽管可能会导致变量遗漏问题。

3、构建方差膨胀因子（$variance\ inflation\ factors$）
$$
VIF_j=\frac{1}{1-R_j^2}
$$
常见的指标是 $VIF$ 不能大于10

误设模型中的方差

回归模型中是否添加某特定变量的判断标准。

真实的回归模型：
$$
y=\beta_0+\beta_1x_1+\beta_2x_2+u
$$
回归模型1：
$$
\hat{y}=\hat{\beta_0}+\hat{\beta_1}x_1+\hat{\beta_2}x_2
$$
回归模型2：
$$
\tilde{y}=\tilde{\beta_0}+\tilde{\beta_1}x_1
$$
通过计算可得：
$$
Var(\hat{\beta_1})=\frac{\sigma^2}{SST_1(1-R_1^2)}
$$

$$
Var(\tilde{\beta_1})=\frac{\sigma^2}{SST_1}
$$

可以看到，$Var(\hat{\beta_1})>Var(\tilde{\beta_1})$（其实不对，因为两个式子中的$\sigma$不一样），可见增加自变量会增加估计量的去方差（至少不会减少）。

考虑如下情况：

若 $\beta_2=0$ ,则：
$$
E(\hat{\beta_1})=\beta_1 \ \ \ E(\tilde{\beta_1})=\beta_1 \
Var(\hat{\beta_1})>Var(\tilde{\beta_1})
$$
这告诉我们不要把无关变量放进模型，无关变量只会加剧共线性问题。

若 $\beta_2 \not=0$ ,则：
$$
E(\hat{\beta_1})=\beta_1 \ \ \ E(\tilde{\beta_1})\not=\beta_1 \
Var(\hat{\beta_1})>Var(\tilde{\beta_1})
$$
这时候就需要进行取舍（$trade\ off$），经济学中一般认为无偏性更加重要一点

估计误差项的方差

我们构造一个估计量：
$$
\hat{\sigma^2}=\frac{\sum_{i=1}^n{\hat{u_i}}^2}{n-k-1}
$$
$n-k-1$为残差变动的自由度，即残差可以自由取值的个数，即当我们给定残差中的$n-k-1$个，余下的$k+1$个便是已知的，$k+1$个限制来自于最小二乘法时$k+1$个限制条件。

定理3.3 $\sigma^2$的无偏估计

由假设$MLR.1-MLR.5$，我们有：
$$
E(\hat{\sigma^2})=\sigma^2
$$

证明：

矩阵证明，暂时略，后续补。

$\hat{\sigma}$ 称为回归标准误（$standard\ error\ of\ the\ regression $）,简称 $ SER $，是误差项标准差的估计值。

$\hat{\beta_j}$的标准差（$standard\ deviation $）为：
$$
sd(\hat{\beta_j})=\sqrt{Var(\hat{\beta_j})}=
\frac{\sigma}{\sqrt{SST_j(1-R_j^2)}}
$$
由于我们无法获得$\sigma$的真实值，故我们需要使用估计值$\hat{\sigma}$进行替换，则：

$\hat{\beta_j}$的标准误($standard\ error$)为：
$$
se(\hat{\beta_j})=\sqrt{\hat{Var}(\hat{\beta_j})}=
\frac{\hat{\sigma}}{\sqrt{SST_j(1-R_j^2)}}
$$
标准误是一个随机变量，来源于样本，当样本确定时，标准误也随之确定。

值得注意的是，标准误的依赖于$Var(\hat{\beta_j})$的公式，而该公式又依赖与同方差假定$MLR.5$。所以如果误差出现异方差性，不会导致$\hat{\beta_j}$的偏误，却会导致对$Var(\hat{\beta_j})$的错误估计。

我们可以对标准误进行变形，得到：
$$
se(\hat{\beta_j})=\frac{\hat{\sigma}}{\sqrt{n}\ sd(x_j)\sqrt{(1-R_j^2)}}
$$
其中，$sd(x_j)=\sqrt{n^{-1}\sum_{i=1}^n(x_{ij}-\bar{x}_j)^2}$，是样本标准差。

$se(\hat{\beta_j})$中的各部分都随$n$的变动而变动，但是$n$越来越大时，除$\sqrt{n}$外各部分均会趋于常数。由此我们知道，标准误大致以$1/ \sqrt{n} $的速率收敛到0。

$OLS$的有效性：高斯-马尔科夫定理（$The\ Gauss-Markov\ Theorem$）

我们需要判断普通最小二乘法（$OLS$）是不是好的，方法是与其他估计值进行比较。我们在比较$OLS$和其他方法估计值时，我们只比较线性估计值，即：
$$
\tilde{\beta_j}=\sum_{i=1}^n{\omega_{ij}y_i}
$$
其中，$w_{ij}$是自变量$x$的函数。

定理3.4

在假定$MLR.1-MLR.5$下，$\hat{\beta_0},\hat{\beta_1},…\hat{\beta_k}$是$\beta_0,\beta_1,…,\beta_k$的最优线性无偏估计量($BLUEs$) ($Best\ Linear\ Unbiased\ Estimators$)

即，在所有线性无偏估计值里面，$OLS$的方差是最小的（因为方差的具体值是随样本变化而变化的，故这里方差最小值的是不管样本如何变化$Var(\hat{\beta_j})<Var(\tilde\beta_j)$恒成立）。该定理说明了使用$OLS$估计多元回归模型的合理性。