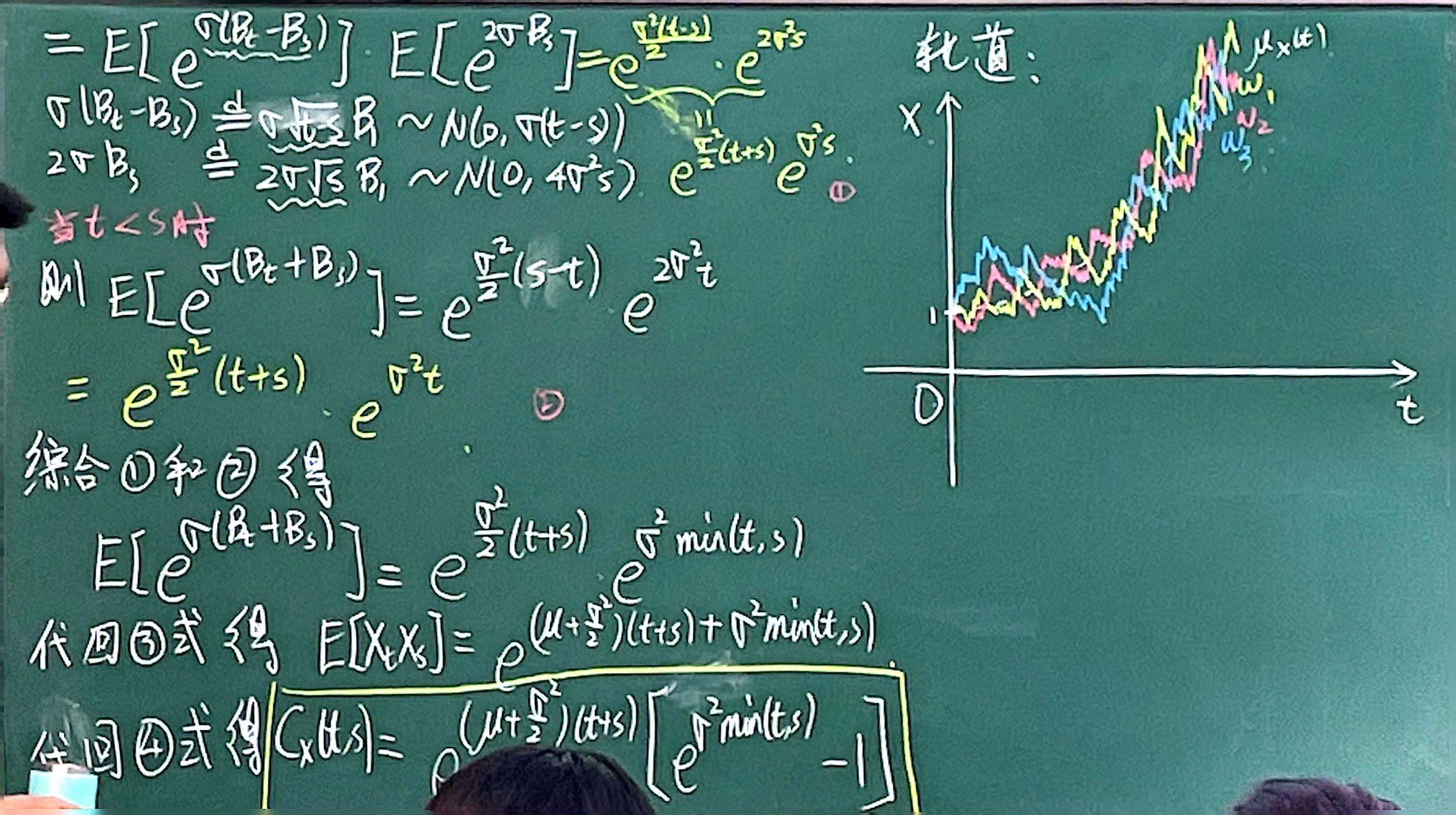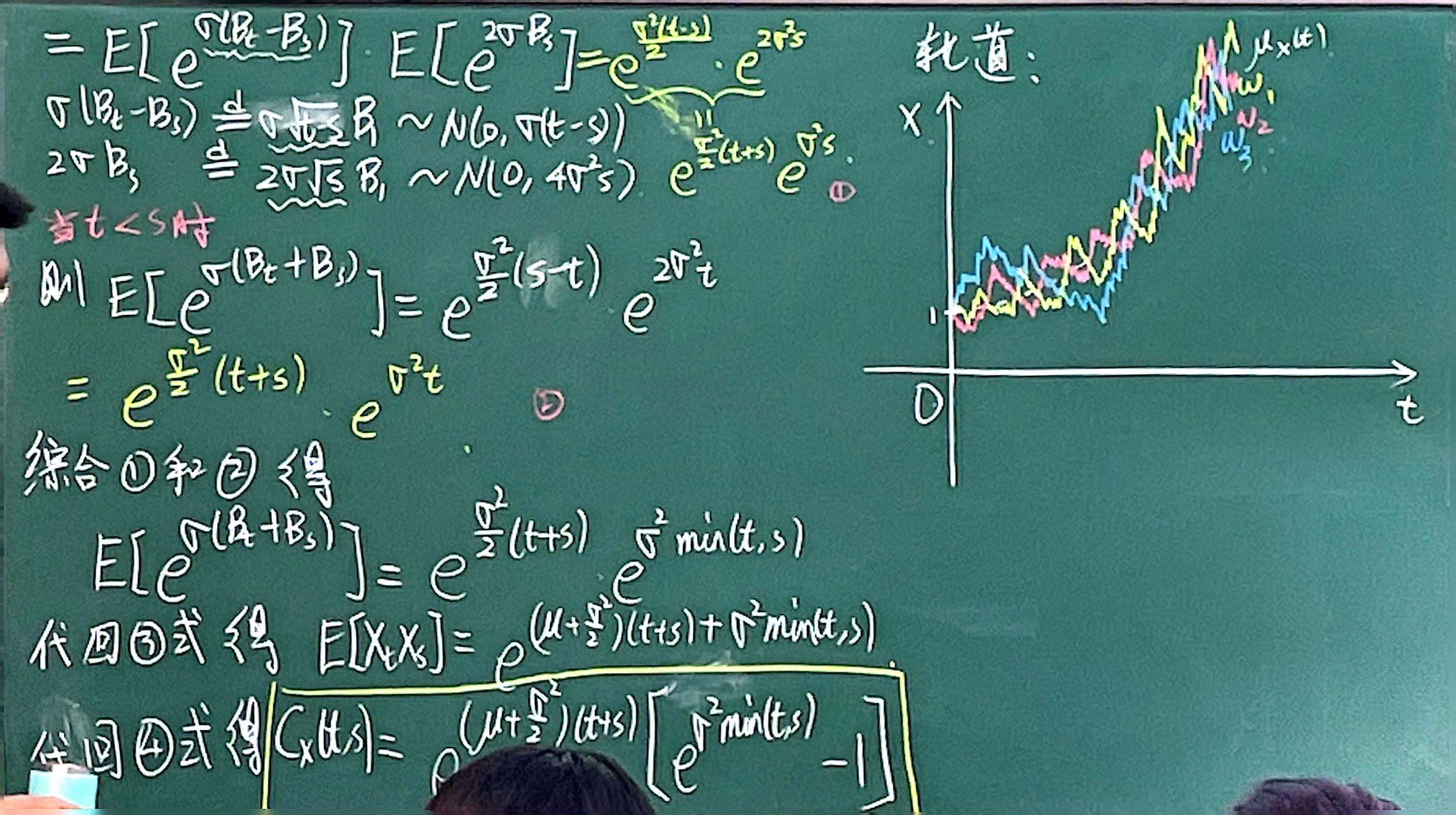布朗运动

定义：

如果随机过程B=(Bt,t≥0)B=(B_t,t \geq 0) ，满足：

  1. 从零点出发，B0=0B_0=0
  2. 具有平稳独立增量
  3. ∀t>0,Bt∼N(0,t)\forall t>0, B_t \sim N(0,t)
  4. 具有连续样本轨道，没有跳跃点

则称 BB 为标准布朗运动（维纳过程（WienerWiener））

有限维分布：

(Bt1,Bt2,...,Btn)(B_{t_1},B_{t_2},...,B_{t_n}) 的分布是高斯分布，因此布朗运动是高斯过程。

* 练习：

求(Bt1,Bt2,...,Btn)(B_{t_1},B_{t_2},...,B_{t_n}) 的分布密度函数中的μ\mu 和 Σ\Sigma

解题思路：BtiB_{t_i}彼此之间不独立，求解很困难，可以变化成独立的各分量，再变化回来

期望

μB(t)=E[Bt]=0\mu_B(t)=E[B_t]=0

方差

σB2(t)=Var(Bt)=t\sigma^2_{B}(t)=Var(B_t)=t

协方差

CB(t,s)=E[BtBs]=min(s,t)C_B(t,s)=E[B_tB_s]=min(s,t)

自相关系数

RB(t,s)=E[BtBs]=min(s,t)R_B(t,s)=E[B_tB_s]=min(s,t)

等价定义

布朗运动是期望值函数为00，协方差函数为min(t,s)min(t,s)的高斯过程。

样本轨道

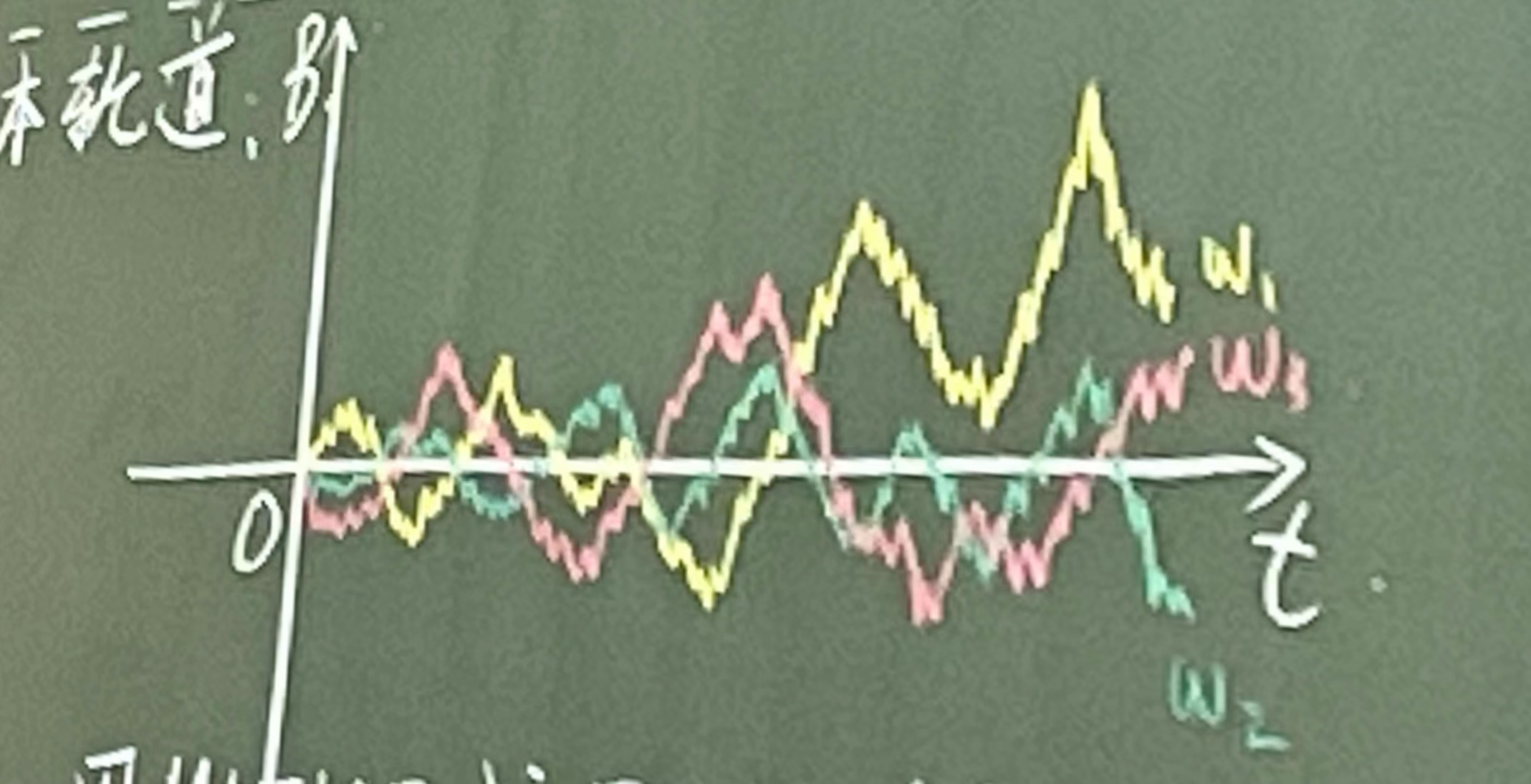
练习

用MATLABMATLAB或PythonPython模拟布朗运动的轨道 T=[0,1],N=1000000T=[0,1], N=1000000

布朗运动几乎必然是处处连续处处不可导

*几乎必然：P(A)=1P(A)=1

H-自相似

对于某个H>0H>0，如果随机过程(Xt,t∈[0,∞])(X_t,t\in[0,\infty])的有限维分布满足：

(aHXt1,aHXt2,...,aHXtn)=d(Xat1,Xat2...Xatn)(a^HX_{t_1},a^HX_{t_2},...,a^HX_{t_n}) \overset{d}{=} (X_{at_{1}},X_{at_{2}}...X_{at_{n}})

对∀a>0,ti≥0,i=1,2..n,n≥1\forall a>0 ,t_i \geq0,i=1,2..n,n \geq 1成立，则称随机过程(Xt,t∈[0,∞])(X_t,t\in[0,\infty])是H-自相似的

性质

对于自相似的随机过程，其轨道几乎必然处处连续处处不可导

布朗运动是0.5-自相似的随机过程

布朗运动的样本轨道在任意有限空间[0,T][0,T]上没有有界变差（全变差无界），即

见书p34

布朗桥(Brownian bridgeBrownian\ bridge)

随机过程：

Xt=Bt−tB1X_t=B_t-tB_1

其中，0≤t≤10\leq t\leq 1

显然：X0=0   ,    X1=0X_0=0\ \ \ ,\ \ \ \ X_1=0。

布朗桥是高斯过程。

μX(t)=0cX(t,s)=min(t,s)−tsσX(t)=t−t2\mu_{X}(t)=0 \\ c_X(t,s)=min(t,s)-ts \\ \sigma_{X}(t)=t-t^2

带漂移项的布朗