【计量经济学（五）】多元回归分析：推断

推断的目的：根基样本估计值来推断真实值

Assumption MLR.6 (Normality of error terms 误差项的正态性)

总体误差$u$独立于解释变量$x_i$，并且服从正态分布。

$u_{i} \sim N(0,\sigma^2)$

以$x$不变作为条件，则$y$的分布也是正态分布

$E(y|x)=E(\beta_0+\beta_1x_1+\beta_2x_2+...+\beta_kx_k+u|x)=\beta_0+\beta_1x_1+\beta_2x_2+...+\beta_kx_k \\Var(y|x)=Var(u|x)= \sigma^2$

所以：

$\pmb{y|x \sim N(\beta_0+\beta_1x_1+\beta_2x_2+...+\beta_kx_k,\sigma^2)}$

$MLR.1-MLR.6$统称为经典线性假定（$CLM$），在这个假定下的模型称为经典线性模型，可以证明，在$CLM$假定下，$OLS$估计量是最小方差无偏估计量。

定理4.1 正态抽样分布

根据$MLR.1-MLR.6$:

$\hat{\beta_{j}} \sim N(\beta_j,Var(\hat{\beta_j}))$

进一步：

$\frac{\hat{\beta_j}-\beta_j}{sd(\hat{\beta_j})} \sim N(0,1)$

证明：

由上一章，我们已知：

$\hat{\beta_j}=\beta_j+\frac{\sum_{i=1}^n\hat{r}_{ij}u_i}{\sum_{i=1}^n\hat{r}_{ij}^2}$

这是关于$u_i$的线性组合，因为$u_i$服从正态分布，故$\hat{\beta_j}$服从正态分布。

定理4.2 标准化估计量的t分布

根据$MLR.1-MLR.6$:

$\frac{\hat{\beta_j}-\beta_j}{se(\hat{\beta_j})} \sim t_{n-k-1}$

证明：

矩阵证明，后续补充。

t分布

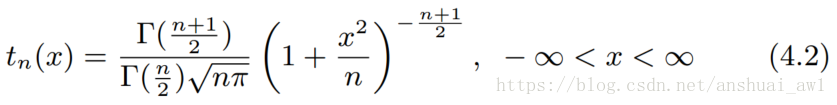
密度函数：

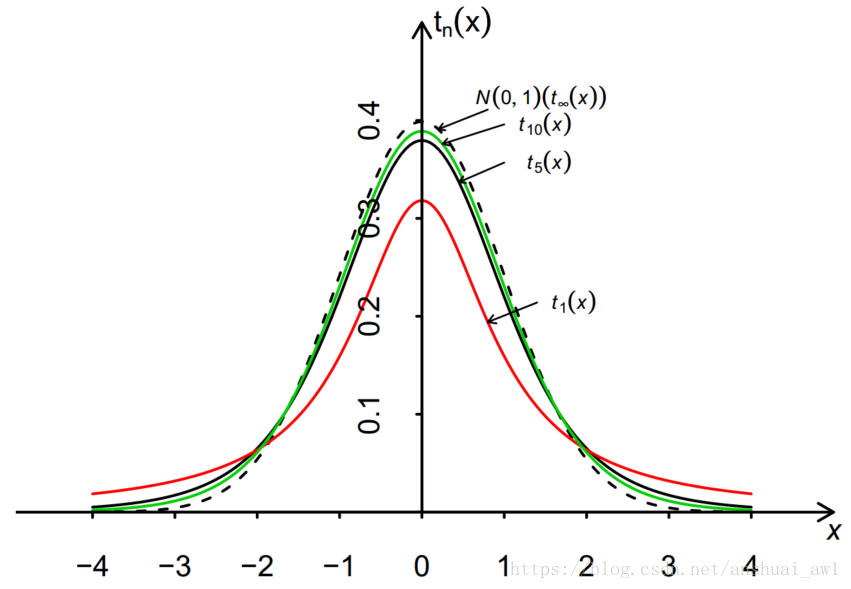
图形为：

如何推断真实值

第一步建立原假设或零假设（$Null \ hypothesis$）

$H_0: \beta_j=0$

第二步构建$t-statistic$（$t$统计量）

$t_{\hat{\beta_j}}=\frac{\hat{\beta_j}}{se(\hat{\beta_j})}$

如何原假设$H_0$成立，则：

$t_{\hat{\beta_j}}=\frac{\hat{\beta_j}}{se(\hat{\beta_j})}=\frac{\hat{\beta_j}-\beta_j}{se(\hat{\beta_j})} \sim t_{n-k-1}$

$t_{\hat{\beta_j}}$是可计算的

假设检验的逻辑：

如果原假设成立，那么t统计量应该服从t分布，我们根据数据计算t统计量，如果t统计量的产生是一个小概率事件，那么拒绝原假设。

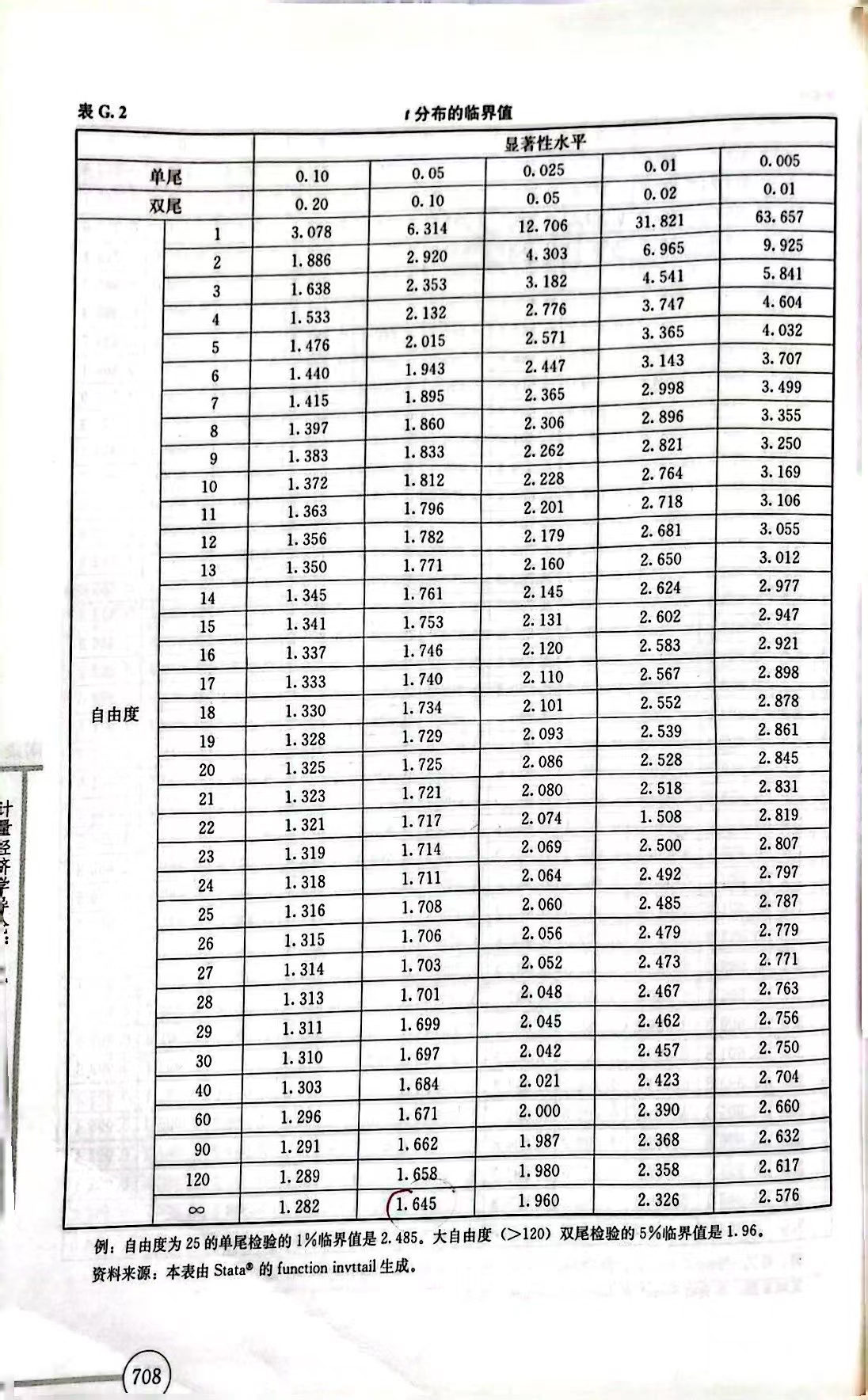
第三步 确定显著性水平和临界值

显著性水平指的是小概率事件发生的概率（当$H_0$正确时拒绝它的概率）。

例如，在5%的显著性水平下，设$c$为$n-k-1$的自由度的$t$分布中处在百分位中第95位的数值，则拒绝法则为

$t_{\beta_j}>c$

单侧备择假设（$Testing\ against\ one-sided\ alternatives$）

第一步提出原假设：

$Test:H_0:\beta_j=0 \ \ \ against\ \ \ \ H_1:\beta_j>0$

第二步计算$t$统计量

第三版根据自由度和显著性水平，计算临界值。

双侧备择假设（$Testing\ against\ two-sided\ alternatives$）

拒绝法则：

$|t_{\hat{\beta_j}}| >c$

如果在一定显著性水平上拒绝$H_0$，我们通常说：$x_j$是统计显著的$(statistically\ significant)$ ，反之，我们则称"$x_j$在显著性水平为$5\%$时是统计上不显著的$(statistically\ insignificant)$"

其他形式的假设

原假设：

$H_0: \ \ \beta_j=a_j$

$t$统计量：

$t=\frac{\hat{\beta_j}-a_j}{se(\hat{\beta_j})}$

计算$t$检验的$p$值

p值的含义：给定$t$统计量的观测值，能拒绝原假设的最小显著性水平

即，显著性（阴影面积）不断减少的过程中，最小的能将$t$统计量包含住的显著性的值；此时，$t$统计量是临界值，$p$为$t$统计量到无穷处积分出的面积。

实践中，我们往往希望更小的显著性水平(显著性水平越小，拒真错误的可能性越小)，因此，$p$值刻画了样本数据能提供的最优（小）的显著性水平。

在双侧假设下：

$p=P(|T|>|t|)$

其中，$T$为自由度为$n-k-1$的$t$分布随机变量，$t$为该检验统计量的数值。

对于一定的显著性水平$\alpha$，若$p<\alpha$，则拒绝原假设；若$p>\alpha$，则在$\alpha$的显著性水平下，就不能拒绝$H_0$.

置信区间（$Confidence\ intervals$）

置信区间：真实值所在的取值范围

在一定显著性水平下（如0.05），可以求得临界值$C_{0.05},-C_{0.05}$（分别是$t$分布的上下2.$5\%$分位数）

故不能拒绝原假设的区间为：

$-C_{0.05}<t_{\hat{\beta}}<C_{0.05}$

$-C_{0.05}<\frac{\hat{\beta_j}-\beta_j}{se(\hat{\beta_j})} <C_{0.05}$

从概率角度：

$P(-C_{0.05}<\frac{\hat{\beta_j}-\beta_j}{se(\hat{\beta_j})} <C_{0.05}) =95\%$

化简得：

$P(\hat{\beta_j}-C_{0.05}se(\hat{\beta_j})<\beta_j{} <\hat{\beta_j}+C_{0.05}se(\hat{\beta_j})) =95\%$

故在$5\%$的显著性水平下，$\beta_j$的置信区间为：

$(\hat{\beta_j}-C_{0.05}se(\hat{\beta_j})\ ,\ \hat{\beta_j}+C_{0.05}se(\hat{\beta_j})\ )$

$a_j \notin interval\ \ \ => \ \ \ reject\ H_0:\beta_j=a_j$

检验关于参数的一个线性组合假设

$log(wage)=\beta_0+\beta_1 jc+\beta_2 univ+\beta_3 exper+u$

如果要检验$\beta_1$是否显示小于$\beta_2$，直觉是$H_0:\beta_1<\beta_2$，但此时$t$统计量为：

$t=\frac{\hat{\beta_1}-\hat{\beta_2}}{se(\hat{\beta_1}-\hat{\beta_2})}$

其分母$se(\hat{\beta_1}-\hat{\beta_2})$无法求得，故考虑换一种方法。

令$H_0: \theta_1=0$ 对$H_1: \theta_1<0$，将$\beta_1=\theta_1+\beta_2$代入原式：

$log(wage)=\beta_0+\theta_1 jc+\beta_2 (jc+univ)+\beta_3 exper+u$

用新变量$totcoll$代替$(jc+univ)$，此时可求得$t$统计量：

$t=\frac{\theta_1}{se(\theta_1)}$

对多个线性约束的检验：F检验

原假设：

$H_0: \beta_{k-q+1}=0,\beta_{k-q+2}=0,...,\beta_{k}=0$

备择假设：

$H_1: \ \ H_0 \ 不成立$

第一步，估计不受约束模型，计算残差平方和$SSR_{ur}$

$y=\beta_0+\beta_1x_1+\beta_2x_2+...+\beta_kx_k+u$

即该模型的残差平方和

第二步，估计受约束模型，计算残差平方和$SSR_r$

$y=\beta_0+\beta_1x_1+\beta_2x_2+...+\beta_{k-q}x_{k-q}+u$

即该模型的残差平方和

第三步，比较残差平方和是不是有很大变化，计算$F$统计量以及做$F$检验。

F统计量（$F-statistic$）

$F=\frac{(SSR_r-SSR_{ur})/q}{SSR_{ur}/(n-k-1)} \sim F_{q,n-k-1}$

其中：$q$为约束条件的个数

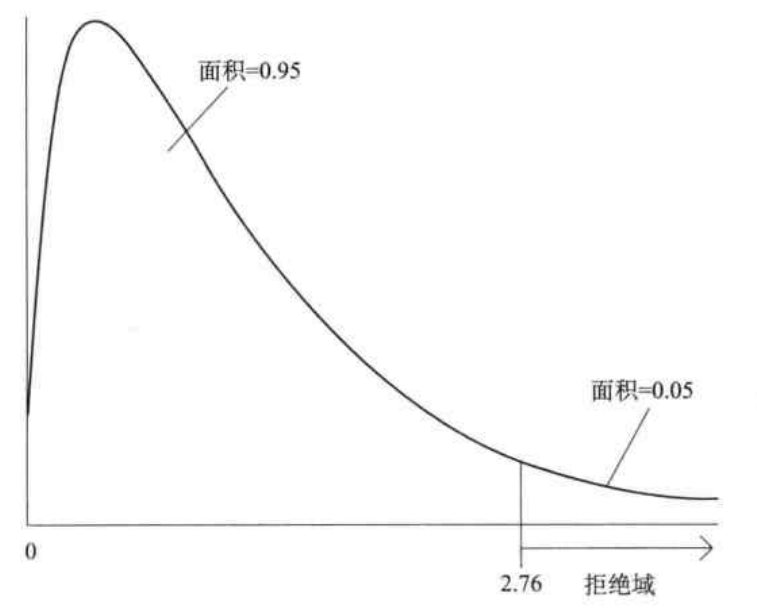
如果拒绝$H_0$，我们就说$x_{k-q+1},...,x_k$在适当的显著性水平上是联合统计显著的，否则是联合不显著的。

对全部系数检验

$H_0: \beta_1=\beta_2=...=\beta_k=0$

不受约束模型中：

$R^2=1-\frac{SSR_{ur}}{SST}$

故:

$SSR_{ur}=SST(1-R^2)$

受约束模型中$R^2=0$，故

$SSR_r =SST$

代入化简得：

$F=\frac{(SSR_r-SSR_{ur})/q}{SSR_{ur}/(n-k-1)}=\frac{R^2/k}{(1-R^2)/(n-k-1)} \sim F_{q,n-k-1}$

此时的显著性称为回归的整体显著性（$overall\ significnace\ of \ the \ regression$）

有时，很小的$R^2$会导致高度显著的$F$统计量，这便解释了我们为什么需要计算$F$统计量来检验联合显著性，而不是仅仅看一下$R^2$的大小。