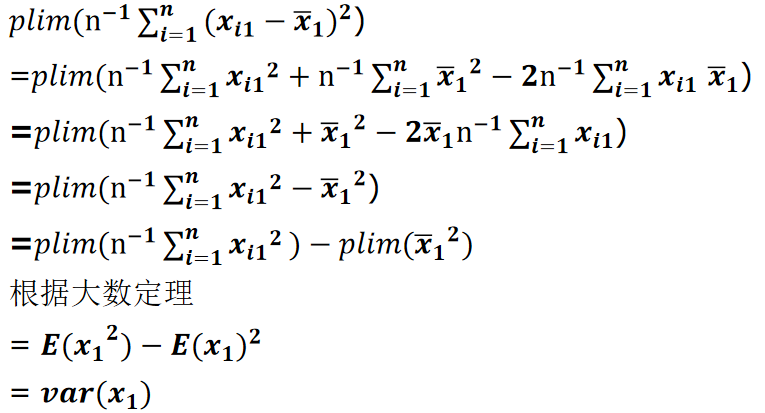Consistency(一致性)：

当样本无限增加时，估计值无限接近真实值。

对于 $\forall\ \epsilon >0$ ，以及 $n \to \infty$，如果
$$
P(|\theta_n-\theta|<\epsilon)\to 1
$$
那么估计$\theta_n$是总体参数$\theta$的一致估计，记为 $plim\ \theta_n=\theta$

定理5.1 OLS的一致性

在假定$MLR.1$到$MLR.4$下，对所有$j=0,1,…k$，$OLS$估计量$\hat{\beta_j}$都是$\beta_j$的一致估计，即 $plim\ \hat{\beta_j}=\beta_j$

对一元回归的证明：

将$y_1=\beta_0+\beta_1 x_{i1}+u_i$代入$\hat{\beta_1}$，可以化简得：
$$
\hat{\beta_1}=\frac{\sum_{i=1}^n(x_{i1}-\bar{x}1)y_i}{\sum{i=1}^n(x_{i1}-\bar{x}1)^2}=\beta_1+\frac{n^{-1}\sum{i=1}^n(x_{i1}-\bar{x}1)u_i}{n^{-1}\sum{i=1}^n(x_{i1}-\bar{x}_1)^2}
$$

再依据大数定理：
$$
plim(n^{-1} \sum_{i=1}^n(x_{i1}-\bar{x}_1)^2)=Var(x_1)
$$

$$
plim(n^{-1} \sum_{i=1}^n(x_{i1}-\bar{x}_1)u_i)=Cov(x_1,u)=E(x_1u)-E(x_1)E(u)=E(x_1u)
$$

证明：

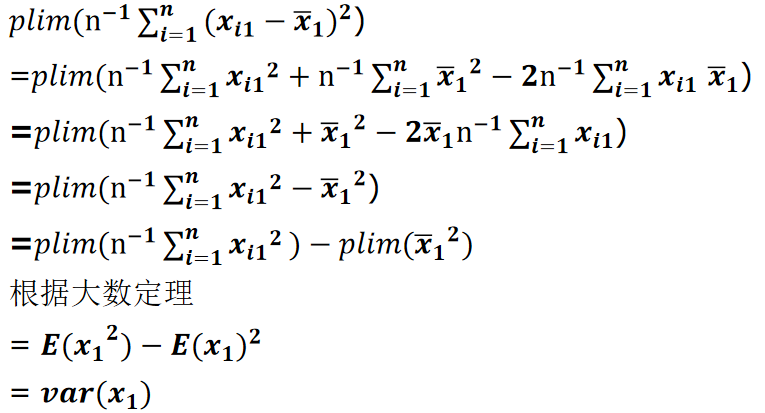
根据假设$MLR.4$ :$E(u|x)=0$，可得$Cov(x_1,u)=0$，故：
$$
plim\ \hat\beta_1 =\beta_1+\frac{Cov(x_1,u)}{Var(x_1)}
=\beta_1
$$

当$Cov(x_1,u) \not =0$时，就会产生不一致性（$Inconsistency$）， 其偏误值wei
$$
plim\ \hat\beta_1 - \beta_1=\frac{Cov(x_1,u)}{Var(x_1)}
$$

假定 $MLR.4’$（零均值和零相关）

对$\forall j=1,2…k$，都有$\pmb{E(u)=0}$ 和 $\pmb{Cov(x_j,u)=0}$

对比假定$MLR.4$ : $\ E(u|x_1,…,x_n)=0 $，可以发现$MLR.4’$是一个更弱的假设，因为：
$$
E(u)=0 \Longrightarrow Cov(x_1,u)=E(x_1u)
=E_{X_1}(E(x_1u|x_1))=E_{X_1}(x_1E(u|x_1))
$$
(这里运用了期望的迭代法则或者说重期望公式)

由上式，当$E(u|x_1)=0$，可以推出 $Cov(x_1,u)=0$ 和 $E(u)=0$，反之不成立。故$MLR.4$是一个更强的假设。

直观上理解：$E(u|x_1)=0$ 以为着$u$和$x_1$的任意形式都不相关，而$Cov(x_1,u)=0$ 仅仅以为这$u$和$x_1$的一次形式不相关，故$E(u|x_1)=0$更严格。

遗漏变量的渐近性类似问题

当变量被遗漏时，自变量会被误放到误差项$u$中，导致其余自变量出现相关性。

真实模型：
$$
y=\beta_0 +\beta_1 x_1+\beta_2 x_2 +v
$$
错误模型：
$$
y =\beta_0 +\beta_1 x_1 +[\beta_2 x_2+v]=\beta_0 +\beta_1x_1+u
$$
于是：
$$
plim\ \hat{\beta_1}=\beta_1 +\frac{Cov(x_1,u)}{Var(x_1)}
=\beta_1 +\beta_2 \frac{Cov(x_1,x_2)}{Var(x_1)}=\beta_1 +\beta_2 \delta
$$

渐近正态与大样本推断

定理5.2 （$Asymptotic\ normality\ of\ OLS$）$OLS$的渐近正态性

在假设$MLR.1-MLR.5$下：
$$
\frac{\hat\beta_j-\beta_j}{se(\hat{\beta_j})} \overset{a}{\sim} N(0,1) \
\frac{\hat\beta_j-\beta_j}{sd(\hat{\beta_j})} \overset{a}{\sim} N(0,1)
$$

$$
plim\ \hat{\sigma}^2=\sigma^2
$$

$$
\sqrt{n}(\hat{\beta_j}-\beta_j) \overset{a}{\sim} N(0,\frac{\sigma^2}{a_j^2})
$$

其中，$a_j^2=plim(n^{-1} \sum_{i=1}^n \hat{r}{ij}^2)$，$\hat{r}{ij}$是$x_j$对其余自变量进行回归所得到的残差。

该定理表明，无论$u$的总体分布如何，合理标准化之后的$OLS$估计量都是近似于服从正态分布的。

在大样本下，$OLS$估计量的方差估计值：
$$
\hat{Var}(\hat{\beta_j})=\frac{\hat{\sigma}^2}{SST_j(1-R_j^2)} \ \ \ \ \ ,j=1,2…k
$$
其中，$SST_j$依概率收敛于 $nVar(x_j)$，

$\hat{\sigma}^2$收敛于$\sigma^2$ , $1-R_j^2$ 收敛于某一个固定值

所以当样本增加时，$n\ \hat{Var}(\hat{\beta_j})$ 收敛于一个常数，或者说：
$$
\hat{Var}(\hat{\beta_j})=\frac{常数}{n}
$$
可以说 $\hat{Var}(\hat{\beta_j})$以$1/n$的速度收敛于0
$$
se(\hat{\beta_j})=\frac{常数}{\sqrt{n}}
$$
标准误以$\sqrt{1/n}$ 的速度收敛于0。

定理5.3 $OLS$的渐近有效性

$$
\sum_{i=1}^n g_j(x_i)(y_i-\tilde{\beta}_0-\tilde{\beta}1 x{i1}-…-\tilde{\beta}k x{ik})=0,j=0,1,…k
$$

在高斯-马尔科夫假定下，令$\tilde{\beta_j}$表示从求解形如上式的方程所得到的估计量，而$\hat{\beta_j}$表示$OLS$估计量。那么，对$j=0,1,2,…,k$，$OLS$估计量具有最小的渐近方差：
$$
Avar\sqrt{n}(\hat{\beta_j}-\beta_j) \leq Avar \sqrt{n}(\tilde{\beta_j}-\beta_j)
$$