定性信息

虚拟变量/哑变量

$$
wage=\beta_0+\delta_0 female+\beta_1 educ+u
$$

虚拟变量：$female$：
$$
female = \begin{cases} 1 , if \ the\ person\ is\ female \ 0 , if \ the\ person\ is\ male \end{cases}
$$

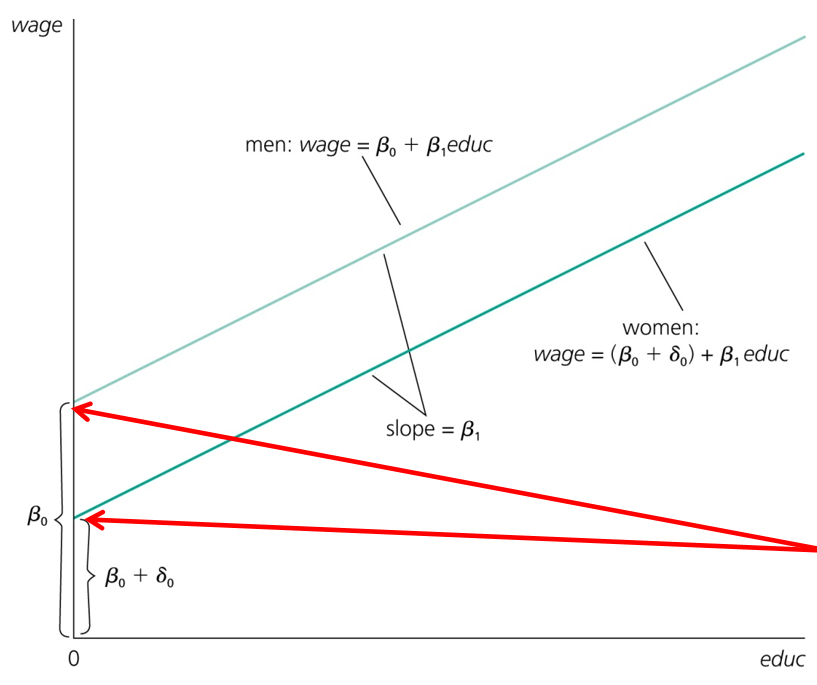
$\delta_0$的含义：给定同等受教育程度，女性和男性在小时工资上的差异。
$$
\delta_0=E(wage|female=1)-E(wage|female=0)
$$

$\delta_0$排除了受教育年限的影响，比如有人辩解称男女薪资差异来源于受教育年限，但$\delta_0$表明即使控制了受教育年限，男女薪资依然存在差异。

虚拟变量陷阱（$Dummy\ varible\ trap $）

不能写成如下方程：
$$
wage=\beta_0+\delta_0 female+\lambda_0 male +\beta_1 educ+u
$$
因为在这种情况下：
$$
female+male=1
$$
而$\beta_0$对应的变量值为1，故具有严格的线性关系，此时回归方程误解。

一种少用但可行的改写方式：
$$
wage=\delta_0 female+\lambda_0 male +\beta_1 educ+u
$$
此时方程有解，但回归系数的含义不好解释，故很少使用。

多类别虚拟变量

$$
\hat{log(wage)}=0.321-0.110female+0.213married-0.301female*married+…
$$

其本质是多个虚拟变量的变形。

多个虚拟变量

四组人：已婚男性、已婚女性、单身男性和单身女性，如果以单身男性为基准组，则其余三个变量的系数都是衡量与单身男性相比的结果。

序数信息变量

数字的大小只起到排序的作用，其绝对差值没有实际意义。如信用评级、排名…

处理方法，对$n$个等级，设置$n-1$个虚拟变量。则$\delta_i$表示与等级为$i$的变量与基准组相比，在$y$上的差异。

例：
$$
MBR=\beta_0+\beta_1 CR+其他因素
$$

$$
MBR=\beta_0+\delta_1 CR_1+\delta_2 CR_2+\delta_3 CR_3+\delta_4 CR_4+其他因素
$$

虚拟变量的交互作用

$$
log(wage)=\beta_0+\delta_0 female+ \beta_1educ+\delta_1 female*educ+u
$$

代入女性$female=1$：
$$
log(wage)=\beta_0+\delta_0+(\beta_1+ \delta_1) educ+u
$$
代入男性$female=0$：
$$
log(wage)=\beta_0=\beta_1 educ +u
$$
所以：
$$
\beta_0 :男性截距项 \
\beta_1 :男性教育对工资的影响 \
\beta_0+\delta_0 :女性的截距项 \
\beta_1+\delta_1 :女性教育对工资的影响
$$
如何检验教育水平对男女工资影响相同？即检验 $\delta_1=0$

如何检验男女工资方程相同？即检验 $\delta_0=0,\delta_1=0$

检验不同组（如男女）之间回归模型的差别

假设有一个影响因素$X$，如何检验$X$对男女的影响是否一致？

在回归方程中加入：
$$
\beta_1 X+\delta_1 female*X
$$
则$X$对男性影响为$\beta_1$，对女性影响为$\beta_1+\delta_1$

注意，截距项也应改为$\beta_0+\delta_0 female$，因为截距项可以理解为恒为1的一个自变量，故也要考虑性别因素。

检验回归模型是否完全无差别需要检验：
$$
H_0: \delta_0=0,\delta_1=1,…,\delta_k=k,
$$
此时使用$F$检验。

二值因变量：线性概率模型

因变量$y$只能取0或1
$$
y=\beta_0+\beta_1x_1+…+\beta_k x_k +u
$$

$$
E(y|x)=\beta_0+\beta_1x_1+…+\beta_k x_k
$$

因为$y$是离散的，只能取0或1，故：
$$
E(y|X)=1P(y=1|x)+0P(y=0|x)=P(y=1|x)
$$
故称为线性概率模型（$LPM$）$(Linear\ probability\ model)$
$$
\beta_j=\frac{\partial P(y=1|x)}{\partial x_j}
$$
当$y$是一个二值变量时，其以$X$为条件的方差为：
$$
Var(y|X)=p(X)[1-p(X)]
$$
其中$p(X)$为成功的概率，即：
$$
p(X)=\beta_0+\beta_1x_1+…+\beta_k x_k
$$