量化投资第二次作业——配对交易策略

原始回测结果分析

根据学号，我分到的是C26C26化学原料及化学制品制造业，但该股票池中有358358支股票，代码运行时间过长（跑一次几十分钟），我就斗胆换成了C28C28化学纤维制造业，初始代码跑出的结果如下：

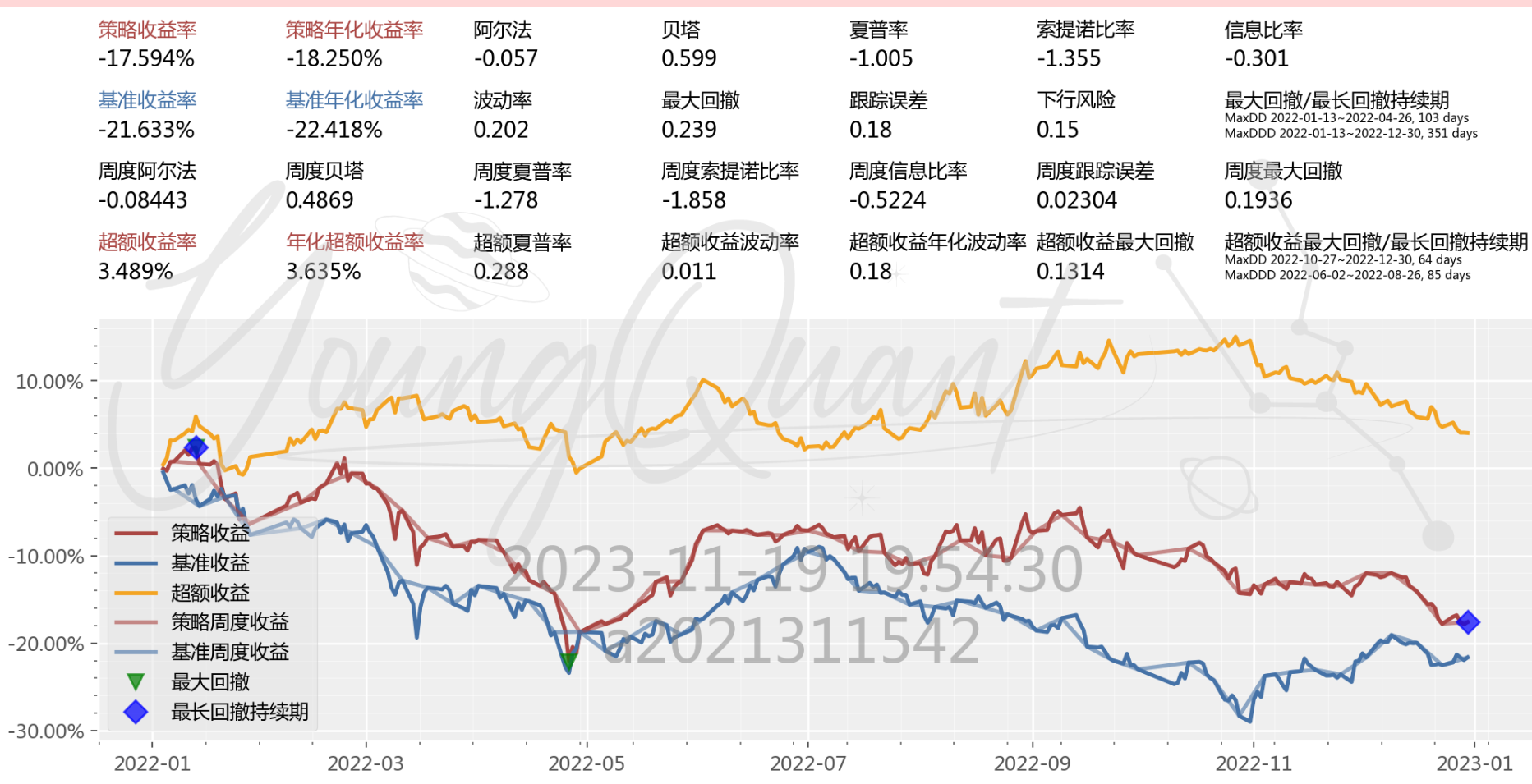
可以看出初始回测的结果并不是很尽如人意，策略收益率为−17.594%-17.594\%，仅仅略高于基准收益率。同时，最大回撤很大，几乎从头回撤到尾。我试着分析这个结果的原因。一个可能的原因是配对交易策略基于两只股票的价差在长期具有均值回复性，当这种均值回复性在短期可能是会出现背离的，也可能回复时间过长，对资产持有者造成很大的压力。因此，我们需要对模型进行优化，是之能够处理短期的背离。于是，我找到了误差修正模型。

误差修正模型

模型原理

协整检验得到的时间序列可以解释变量之存在的长期关系，但却忽略了协整变量之间可能存在的短期偏离现象，这种短暂偏离可以使用误差修正模型(ErrorCorrectionModelError Correction Model) 进行修正。误差修正模型 (简称 ECMECM模型) 于 1978 年由$ Davidson、、Hendrt、、Srba$ 和 YeoYeo四位学者提出，因此该模型亦被称为 $DHSY $模型。一阶误差修正模型推导如下：

假定时间序列{Xt}\{X_t \} 和 {Yt}\{Y_t\}之间具有协整关系，其表达式为：

Yt=α0+α1Xt+εtY_t=\alpha_0+\alpha_1 X_t+\varepsilon_t

其中，α1\alpha_1为YtY_t关于XtX_t的长期系数 (即：协整系数)，但是在金融市场中，会出现很多非均衡状态。可以用一阶滞后自回归模型来描述这种关系，假设关系表达式如下：

Yt=β0+β1Xt+β2Xt−1+μYt−1+εtY_t=\beta_0+\beta_1 X_t+\beta_2X_{t-1}+\mu Y_{t-1}+\varepsilon_t

其中，β1\beta_1为YtY_t关于XtX_t的短期系数，εt\varepsilon_t是均值为00、方差为σ2\sigma^2的白噪声序列。该模型说明YtY_t的取值不仅与XtX_t的取值有关，还与Xt−1X_{t-1}的取值有关。再对上式进行差分处理，可以整理得到：

ΔYt=β1ΔXt−λ(Yt−1−α1′Xt−1−α0′)+εt\Delta Y_t=\beta_1 \Delta X_t-\lambda(Y_{t-1}-\alpha_1'X_{t-1}-\alpha_0')+\varepsilon_t

其中：

λ=1−μ,   α0′=β01−μ,   α1′=β1+β21−μ\lambda=1-\mu,\ \ \ \alpha'_0=\frac{\beta_0}{1-\mu},\ \ \ \alpha_1'=\frac{\beta_1+\beta_2}{1-\mu}

记t−1t-1期的误差修正项为：

ecmt−1=Yt−1−α1′Xt−1−α0′ecm_{t-1}=Y_{t-1}-\alpha_1' X_{t-1}-\alpha_0'

则一阶误差修正模型可表示为：

ΔYt=β1ΔXt−λecmt−1+εt\Delta Y_t=\beta_1 \Delta X_t-\lambda ecm_{t-1} +\varepsilon_t

其中，误差修正项的系数 0<λ<10 <λ < 1，反映了对于短期偏离均衡关系的调整强度。ecmt−1ecm_{t-1}的修正作用为：当Yt−1Y_{t-1}大于其长期均衡α1′Xt−1+α0′\alpha_1' X_{t-1}+\alpha_0'的值（即：ecmt−1ecm_{t-1}为正）时，−λ ecmt−1-\lambda\ ecm_{t-1}为负，可以使ΔYt\Delta Y_t减小，从而使得YtY_t值向均衡水平回归；当Yt−1Y_{t-1}小于其长期均衡α1′Xt−1+α0′\alpha_1' X_{t-1}+\alpha_0'的值（即：ecmt−1ecm_{t-1}为负）时，−λ ecmt−1-\lambda\ ecm_{t-1}为正，可以使ΔYt\Delta Y_t增大，从而使得YtY_t值向均衡水平回归。以此，可以起到修正作用。

代码介绍

我们首先照旧进行协整性检验，得到具有协整性的股票对，这些股票对具有稳定的长期关系。在此基础上，对这些股票对应用误差修正模型，以解决其短期偏离的问题。

在代码中，我们采用如下表达式：

ΔYt=β0+β1ΔXt−(1−μ)Y−1+(β1+β2)X−1+εt\Delta Y_t=\beta_0+\beta_1 \Delta X_t-(1-\mu)Y_{-1}+(\beta_1+\beta_2)X_{-1}+\varepsilon_t

其中，ΔYt\Delta Y_t代表股票YY一阶差分后的对数价格，ΔXt\Delta X_t代表股票YY一阶差分后的对数价格，Y−1Y_{-1}代表股票YY的一阶滞后，X−1X_{-1}代表股票XX的一阶滞后。

具体的求解方法就是以ΔYt\Delta{Y_t}为因变量，ΔXt\Delta X_t、Y−1Y_{-1}、X−1X_{-1}为自变量进行OLSOLS多元回归，相关代码如下：

回归代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
for pair in pairs:
    #取得协整股票对的代码
    stock_sample1 = stock_prices[pair[0]]
    stock_sample2 = stock_prices[pair[1]]
    ###############
    y = np.log(stock_sample1)
    x = np.log(stock_sample2)
    data = pd.DataFrame({'y': y, 'x': x})
    # 差分
    data_diff = data.diff().dropna()
    # 添加截距项和滞后项
    data_diff['const'] = 1
    data_diff['y_lag'] = data['y'].shift(1)
    data_diff['x_lag'] = data['x'].shift(1)
    # 构建误差修正模型
    model = sm.OLS(data_diff['y'], data_diff[['const', 'x', 'y_lag', 'x_lag']])
    result = model.fit()
    r_squared = result.rsquared
   	# print(f"R平方值: {r_squared}")
    # 打印模型概要
  	#  print(result.summary())
    yy = y[1:]
    #计算回归残差的标准差，也就是说diff是残差序列的标准差
    diff_std = np.std(yy - result.predict())
    # 将回归得到的数据存下来，依次是常数项，系数项，diff
    context.ols_result[pair] = (result.params[0], result.params[1], result.params[2], result.params[3], diff_std,r_squared)

通过观察拟合优度R2R^2，我发现误差修正模型的拟合优度普遍低于之前的一元回归，部分情况R2R^2过低，需要进行剔除，故我对回归结果进行筛选，只选取R2R^2大于0.30.3进行交易，代码如下：

1
2
ppairs = context.ols_result.keys()
pairs = [pair for pair in ppairs if context.ols_result[pair][5]>=0.3 ]
交易代码：

和原始的代码一样，我也是将观察值与估计值作差得到误差项，根据误差项的大小进行决策。误差项的计算代码如下：

1
2
3
4
5
6
7
8
stock_de, stock_inde = pair # 当pairs里还有pvalue的时候，需要调整写法
price_dep = np.log(history_bars(stock_de, 2, '1d','close'))
price_inde = np.log(history_bars(stock_inde, 2, '1d', 'close'))
#残差序列突破一倍标准差开仓
const, beta1, beta2, beta3,diff,rr = context.ols_result[pair]
# print('R-square==',rr)
conds = (price_dep[0]-price_dep[1]) - const - beta1*(price_inde[0]-price_inde[1])-beta2*price_dep[1]-beta3*price_inde[1]
#  print('conds=',conds,'   diff=',diff)

优化结果分析

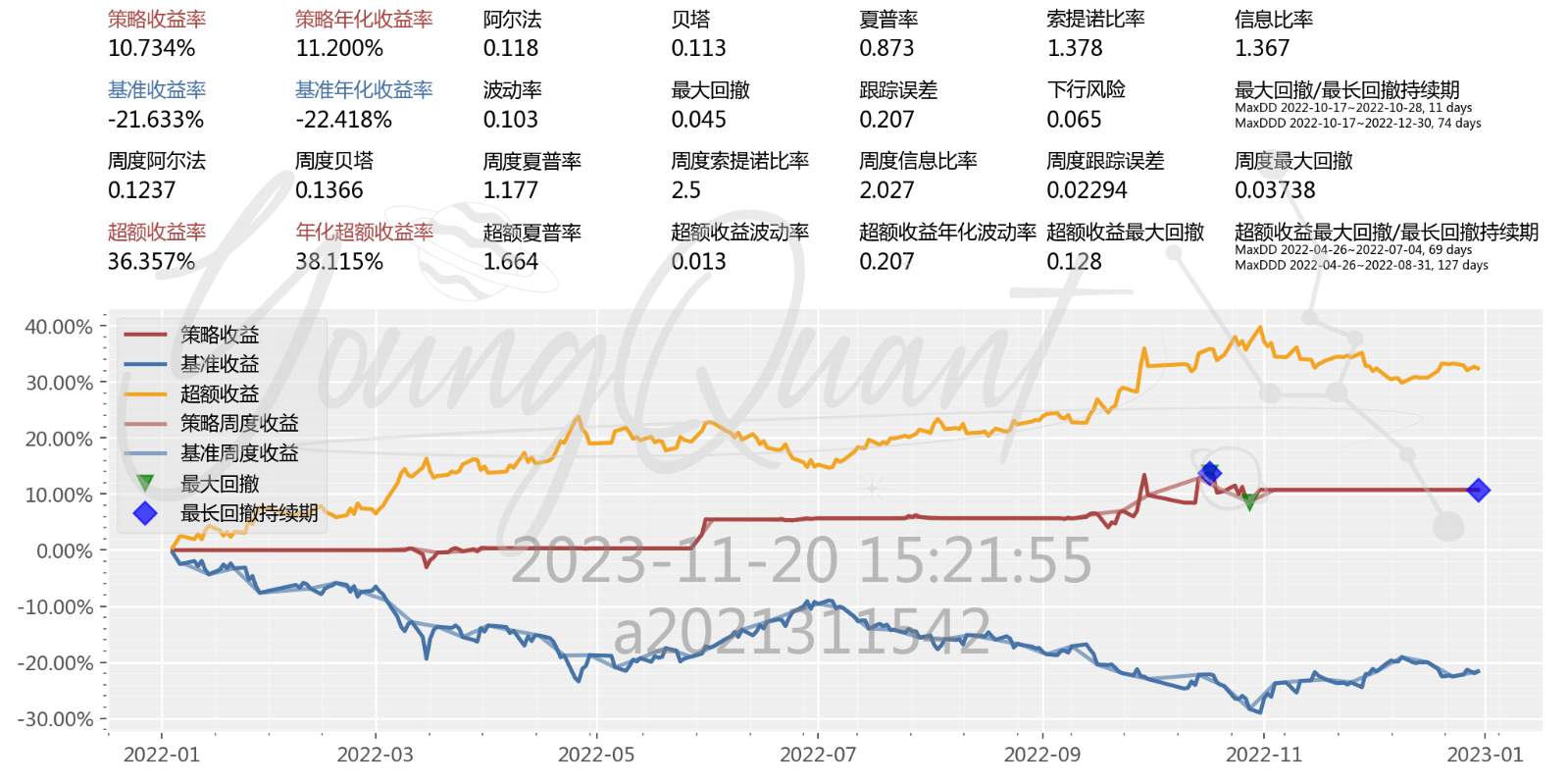
可以看出，经过优化之后策略的收益率有了明显的提升，同时最大回撤与最大回撤持续期都有效降低。其他指标如波动率、阿尔法、贝塔、夏普率等也有一定的提升。另一个明显的差异是策略收益曲线较之前变得更加“平稳”了，究其原因，可能是误差修正模型进行了第二次筛选，使得满足配对要求的股票对进一步减少，进而交易的频率减少了，某种方面来说提高了交易的“质量”；另一方面，新模型的交易信号可能还有改进的空间，或许不应该以一倍的标准差为界限，可能存在更独特的交易信号。

完整代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
from youngquant.api import *
from youngquant import exec_strategy
import statsmodels.api as sm
import numpy as np
import pandas as pd
from itertools import combinations
pd.set_option('display.max_rows',None)
pd.set_option('display.max_columns',None)
config = {
  "base": {
    "start_date": "2022-01-01",
    "end_date": "2022-12-31",
    "frequency": "1d",
    "benchmark": "000300.XSHG",
    "accounts": {
        "stock": 1000000
    }
  },
  "extra": {
    "log_level": "error",
  },
  "mod": {
    "sys_analyser": {
      "enabled": True,
      "plot": True
    },
    "mongodb": {
        "enabled": True,
    }
  }
}
# 工具函数
def find_cointegrated_pairs(stock_prices:dict):
    '''用途：获取强协整股票组及P值'''  
    stock_lists = stock_prices.keys()
    # 所有可能的股票组合
    all_pairs = combinations(stock_lists, 2)
    # 如果不用 pvalue 进行仓位分配

    pairs = [pair for pair in all_pairs if sm.tsa.stattools.coint(stock_prices[pair[0]], stock_prices[pair[1]])[1] < 0.01]
    # 记录 pvalue
    # pairs = []
    # for pair in all_pairs:
    #     # 获取相应的两只股票的价格Series
    #     stock1 = stock_prices[pair[0]]
    #     stock2 = stock_prices[pair[1]]
    #     # 分析它们的协整关系
    #     result = sm.tsa.stattools.coint(stock1, stock2)
    #     # 取出并记录p值
    #     pvalue = result[1]
    #     if pvalue < 0.01:
    #         # 记录股票对和相应的p值
    #         pairs.append((pair[0], pair[1], pvalue))
    return pairs


def find_stock_pairs(context, bar_dict):
    # 初始化以及重置变量
    context.ols_result = {}  # 记录强协整关系股票对以及回归的结果，结构  {(stock1, stock2): (const, coe, diff)}
    context.stock_pos = {}  # 记录股票仓位，结构  {(stock1, stock2): (1 or 0, 1 or 0)}，0表示空，1表示多，还没完全设计好
    context.tag = {}
    stock_list = list(industry(context.industry))
    stock_prices = {}  # 记录股票的收盘价序列，结构  {stock: ndarray}
  #  print('len_stock_list=',len(stock_list))
    for stock in stock_list:
        # 不够细致，可能存在股票停牌情况，是否需要改进？
        # 获取股票上市天数，*1.4是把观测日（交易日）转化为日历日天数，+7是为了更加确保能拿到context.observation条数据
        if instruments(stock).days_from_listed() > (context.observation*1.4 + 7):
            price_close = history_bars(stock, context.observation, '1d', 'close')
            stock_prices[stock] = price_close
        else:
            logger.info(stock + 'is out of date...')
    #获得强协整性股票对
   # print(len(stock_prices))
   # print(stock_prices)
  #  log_stock_prices = {key: np.log(value) for key, value in stock_prices.items()}
    pairs = find_cointegrated_pairs(stock_prices) 
    logger.info(pairs)
    if len(pairs) > 0:        
        for pair in pairs:
            #取得协整股票对的代码
            stock_sample1 = stock_prices[pair[0]]
            stock_sample2 = stock_prices[pair[1]]
            ###############
            y = np.log(stock_sample1)
            x = np.log(stock_sample2)
            data = pd.DataFrame({'y': y, 'x': x})
            # 差分
            data_diff = data.diff().dropna()
          #  print('len_data=',len(data))
          #  print('len_data_diff=',len(data_diff))
            # 添加截距项和滞后项
            data_diff['const'] = 1
            data_diff['y_lag'] = data['y'].shift(1)
            data_diff['x_lag'] = data['x'].shift(1)
          #  print('len_data_diff[x_lag]=',len(data_diff['x_lag']))
          #  print('len_data_diff[const]=',len(data_diff['const']))
            # 构建误差修正模型
            model = sm.OLS(data_diff['y'], data_diff[['const', 'x', 'y_lag', 'x_lag']])
            result = model.fit()
            r_squared = result.rsquared
           # print(f"R平方值: {r_squared}")
            # 打印模型概要
          #  print(result.summary())
            yy = y[1:]
            #计算回归残差的标准差，也就是说diff是残差序列的标准差
            diff_std = np.std(yy - result.predict())
            # 将回归得到的数据存下来，依次是常数项，系数项，diff
            context.ols_result[pair] = (result.params[0], result.params[1], result.params[2], result.params[3], diff_std,r_squared)

def sink_stock(context, bar_dict):
    '''当前处理方式会增加交易成本'''
    for stock in context.portfolio.positions:
        order_target_percent(stock, 0)

def initialize(context):
    context.industry = 'C28'
    context.observation = 60
    context.counter = 0
    #每月运行更新寻找协整股票对
    scheduler.run_monthly(find_stock_pairs, tradingday=1, time_rule='before_trading')
    #每月没有了结的仓位在更新协整股票时清仓
    scheduler.run_monthly(sink_stock, tradingday=1, time_rule=market_open(hour=0))
    
def before_trading_start(context):
    context.counter=0  # 分钟回测才会用得到
    pass

def handle_data(context, bar_dict):
    context.counter += 1
    # 避开前10分钟，留着分钟回测时用
    if context.counter >= 0:
        #取得股票对的代码
        ppairs = context.ols_result.keys()
        pairs = [pair for pair in ppairs if context.ols_result[pair][5]>=0.3 ]

        order_number = len(pairs)
        #print(len(ppairs),'  ',len(pairs))
        #logger.info(pairs)
        #确定股票对的数量，便于后面等权重分配下单资金
        for pair in pairs:
            stock_de, stock_inde = pair # 当pairs里还有pvalue的时候，需要调整写法
            price_dep = np.log(history_bars(stock_de, 2, '1d','close'))
            price_inde = np.log(history_bars(stock_inde, 2, '1d', 'close'))
            #残差序列突破一倍标准差开仓
            #  const, coe, diff = context.ols_result[pair]
            const, beta1, beta2, beta3,diff,rr = context.ols_result[pair]
   
            # print('R-square==',rr)
            conds = (price_dep[0]-price_dep[1]) - const - beta1*(price_inde[0]-price_inde[1])-beta2*price_dep[1]-beta3*price_inde[1]
            #  print('conds=',conds,'   diff=',diff)
            if conds > diff:
                order_target_percent(stock_de, 0)
                order_target_percent(stock_inde, 1/order_number)
                # 突破一倍标准差，卖出股票y，买入股票x。
                context.stock_pos[pair] = (0, 1)
            #残差序列跌破负一倍标准差开仓
            if conds < -diff:
                order_target_percent(stock_inde, 0)
                order_target_percent(stock_de, 1/order_number)
                context.stock_pos[pair] = (1, 0)
                
exec_strategy(initialize=initialize,before_trading_start=before_trading_start,handle_data=handle_data,config=config)